Refining Self-Supervised Learning in Imaging: Beyond Linear Metric
Paper and Code
Feb 25, 2022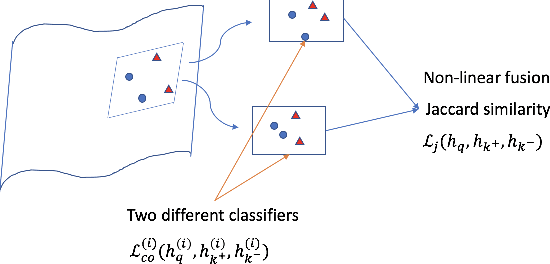
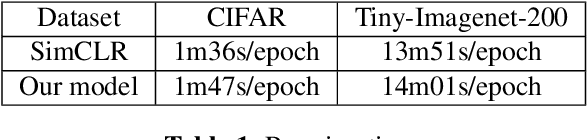
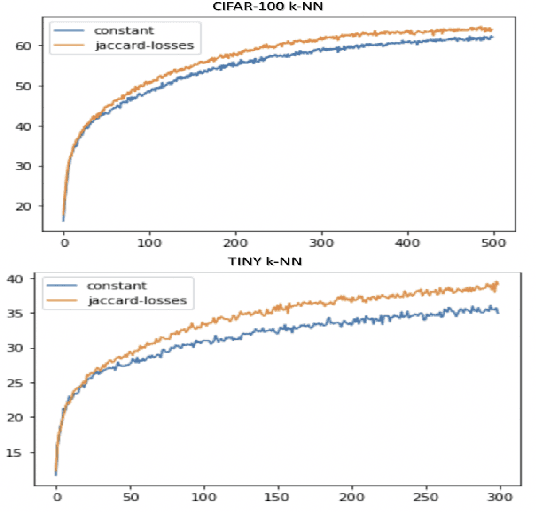
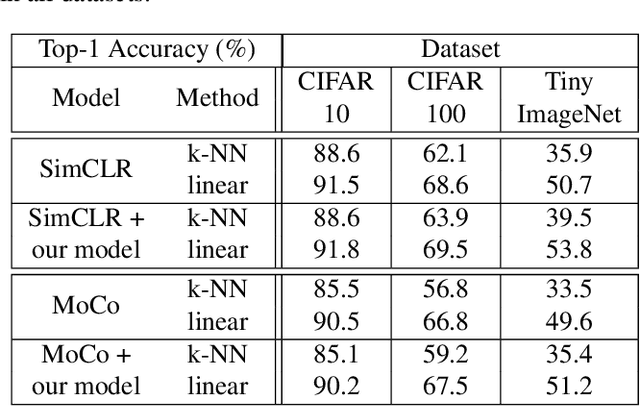
We introduce in this paper a new statistical perspective, exploiting the Jaccard similarity metric, as a measure-based metric to effectively invoke non-linear features in the loss of self-supervised contrastive learning. Specifically, our proposed metric may be interpreted as a dependence measure between two adapted projections learned from the so-called latent representations. This is in contrast to the cosine similarity measure in the conventional contrastive learning model, which accounts for correlation information. To the best of our knowledge, this effectively non-linearly fused information embedded in the Jaccard similarity, is novel to self-supervision learning with promising results. The proposed approach is compared to two state-of-the-art self-supervised contrastive learning methods on three image datasets. We not only demonstrate its amenable applicability in current ML problems, but also its improved performance and training efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge