Efficient and Effective Methods for Mixed Precision Neural Network Quantization for Faster, Energy-efficient Inference

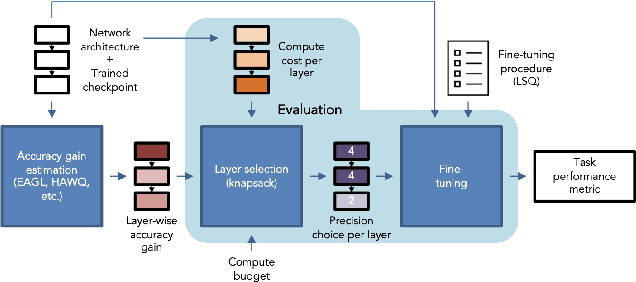
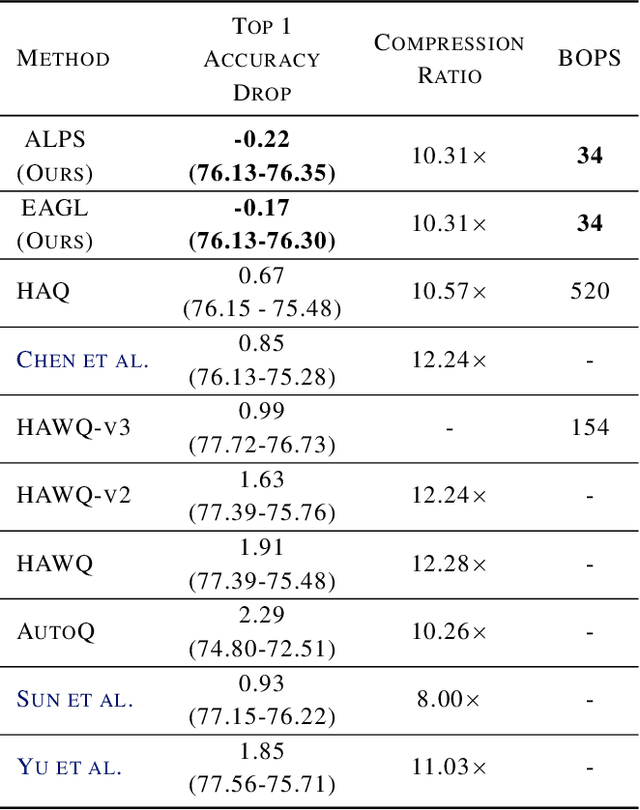
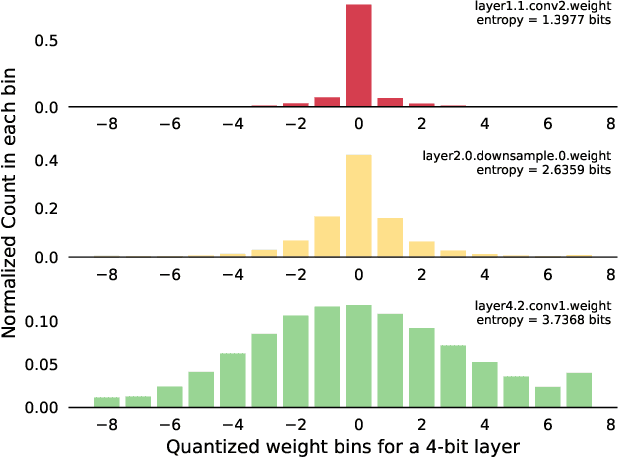
For effective and efficient deep neural network inference, it is desirable to achieve state-of-the-art accuracy with the simplest networks requiring the least computation, memory, and power. Quantizing networks to lower precision is a powerful technique for simplifying networks. It is generally desirable to quantize as aggressively as possible without incurring significant accuracy degradation. As each layer of a network may have different sensitivity to quantization, mixed precision quantization methods selectively tune the precision of individual layers of a network to achieve a minimum drop in task performance (e.g., accuracy). To estimate the impact of layer precision choice on task performance two methods are introduced: i) Entropy Approximation Guided Layer selection (EAGL) is fast and uses the entropy of the weight distribution, and ii) Accuracy-aware Layer Precision Selection (ALPS) is straightforward and relies on single epoch fine-tuning after layer precision reduction. Using EAGL and ALPS for layer precision selection, full-precision accuracy is recovered with a mix of 4-bit and 2-bit layers for ResNet-50 and ResNet-101 classification networks, demonstrating improved performance across the entire accuracy-throughput frontier, and equivalent performance for the PSPNet segmentation network in our own commensurate comparison over leading mixed precision layer selection techniques, while requiring orders of magnitude less compute time to reach a solution.

Learned Step Size Quantization

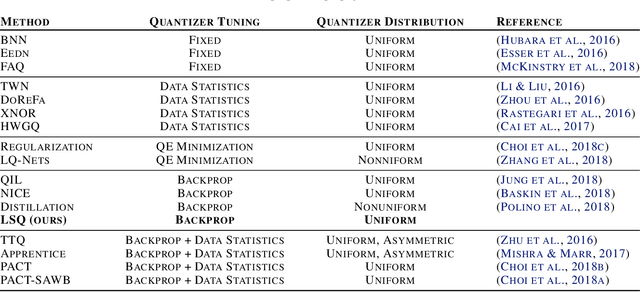
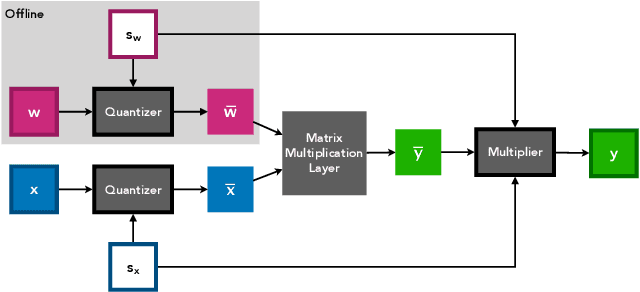
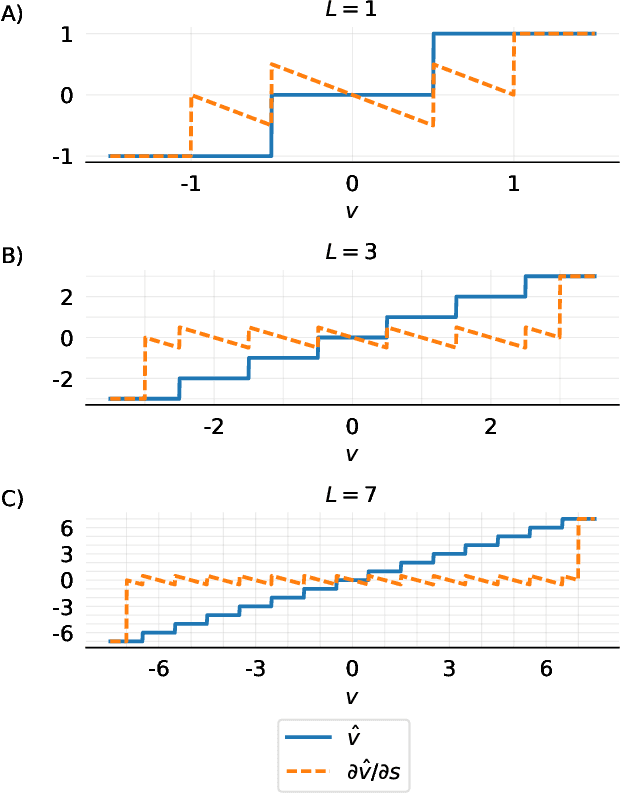
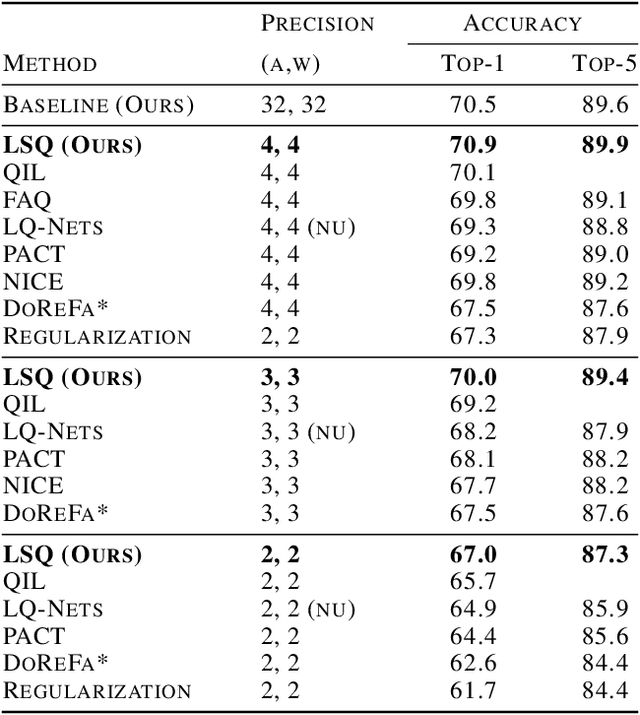
We present here Learned Step Size Quantization, a method for training deep networks such that they can run at inference time using low precision integer matrix multipliers, which offer power and space advantages over high precision alternatives. The essence of our approach is to learn the step size parameter of a uniform quantizer by backpropagation of the training loss, applying a scaling factor to its learning rate, and computing its associated loss gradient by ignoring the discontinuity present in the quantizer. This quantization approach can be applied to activations or weights, using different levels of precision as needed for a given system, and requiring only a simple modification of existing training code. As demonstrated on the ImageNet dataset, our approach achieves better accuracy than all previous published methods for creating quantized networks on several ResNet network architectures at 2-, 3- and 4-bits of precision.

Low Precision Policy Distillation with Application to Low-Power, Real-time Sensation-Cognition-Action Loop with Neuromorphic Computing

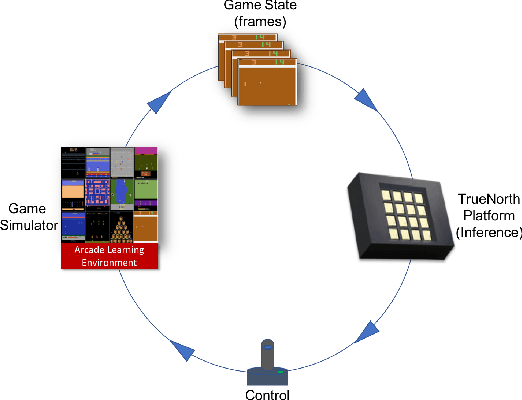
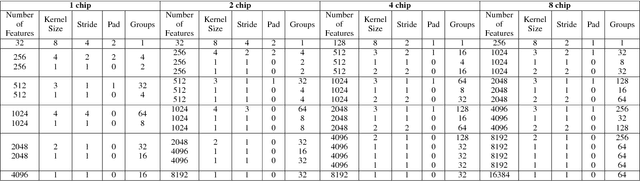
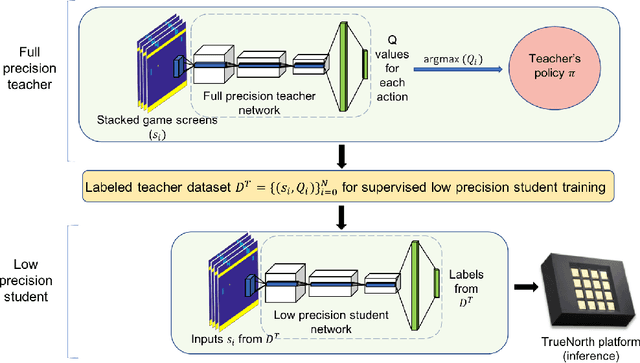
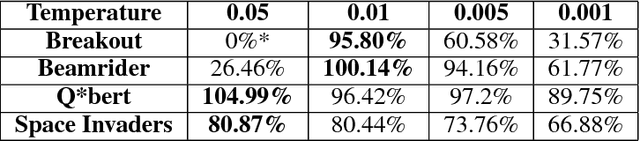
Low precision networks in the reinforcement learning (RL) setting are relatively unexplored because of the limitations of binary activations for function approximation. Here, in the discrete action ATARI domain, we demonstrate, for the first time, that low precision policy distillation from a high precision network provides a principled, practical way to train an RL agent. As an application, on 10 different ATARI games, we demonstrate real-time end-to-end game playing on low-power neuromorphic hardware by converting a sequence of game frames into discrete actions.

Discovering Low-Precision Networks Close to Full-Precision Networks for Efficient Embedded Inference

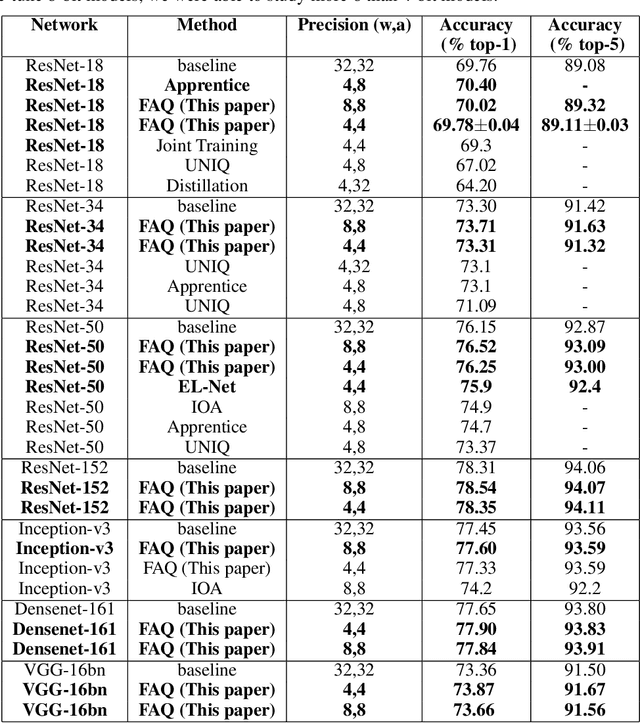
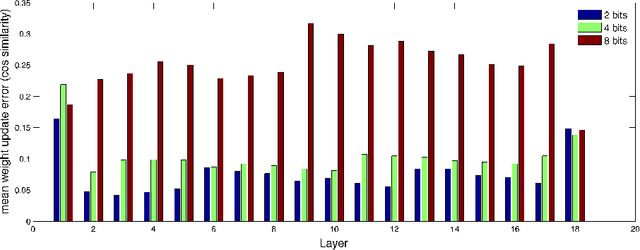
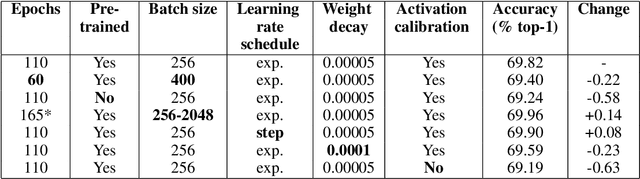
To realize the promise of ubiquitous embedded deep network inference, it is essential to seek limits of energy and area efficiency. To this end, low-precision networks offer tremendous promise because both energy and area scale down quadratically with the reduction in precision. Here, for the first time, we demonstrate ResNet-18, ResNet-34, ResNet-50, ResNet-152, Inception-v3, densenet-161, and VGG-16bn networks on the ImageNet classification benchmark that, at 8-bit precision exceed the accuracy of the full-precision baseline networks after one epoch of finetuning, thereby leveraging the availability of pretrained models. We also demonstrate for the first time ResNet-18, ResNet-34, and ResNet-50 4-bit models that match the accuracy of the full-precision baseline networks. Surprisingly, the weights of the low-precision networks are very close (in cosine similarity) to the weights of the corresponding baseline networks, making training from scratch unnecessary. The number of iterations required by stochastic gradient descent to achieve a given training error is related to the square of (a) the distance of the initial solution from the final plus (b) the maximum variance of the gradient estimates. By drawing inspiration from this observation, we (a) reduce solution distance by starting with pretrained fp32 precision baseline networks and fine-tuning, and (b) combat noise introduced by quantizing weights and activations during training, by using larger batches along with matched learning rate annealing. Together, these two techniques offer a promising heuristic to discover low-precision networks, if they exist, close to fp32 precision baseline networks.