Learned Step Size Quantization
Paper and Code
Feb 21, 2019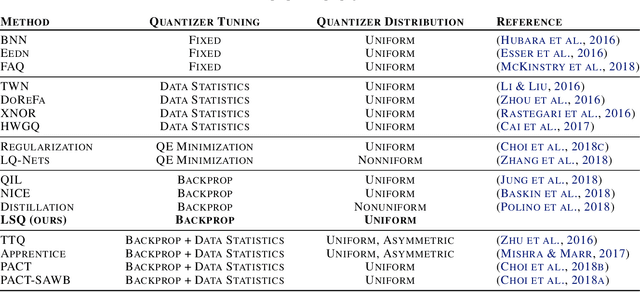
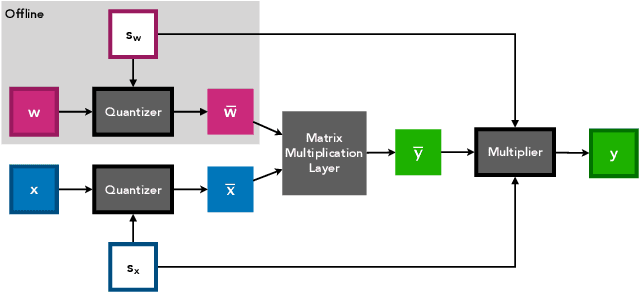
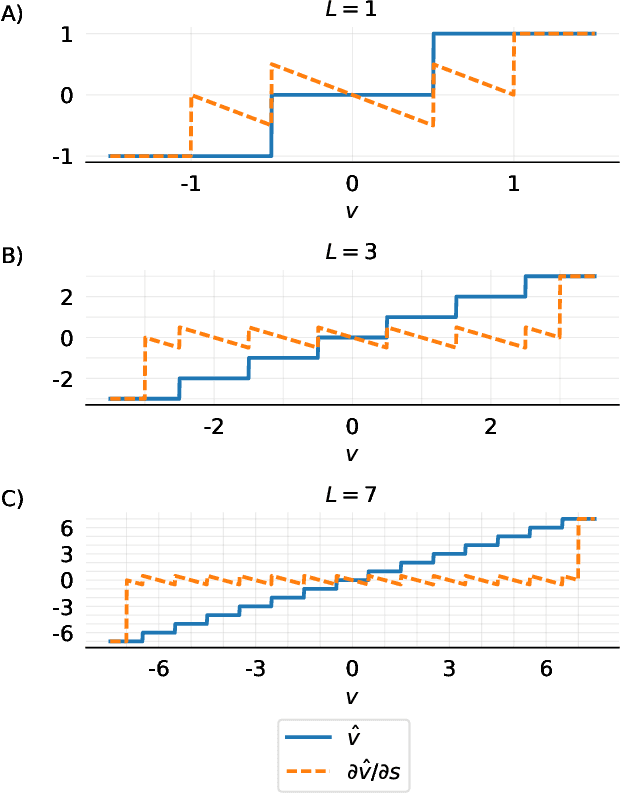
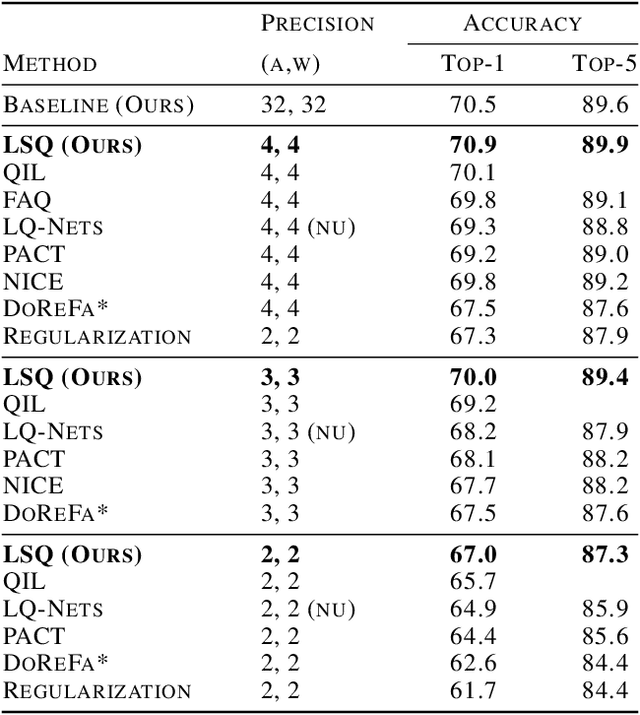
We present here Learned Step Size Quantization, a method for training deep networks such that they can run at inference time using low precision integer matrix multipliers, which offer power and space advantages over high precision alternatives. The essence of our approach is to learn the step size parameter of a uniform quantizer by backpropagation of the training loss, applying a scaling factor to its learning rate, and computing its associated loss gradient by ignoring the discontinuity present in the quantizer. This quantization approach can be applied to activations or weights, using different levels of precision as needed for a given system, and requiring only a simple modification of existing training code. As demonstrated on the ImageNet dataset, our approach achieves better accuracy than all previous published methods for creating quantized networks on several ResNet network architectures at 2-, 3- and 4-bits of precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge