Discovering Low-Precision Networks Close to Full-Precision Networks for Efficient Embedded Inference

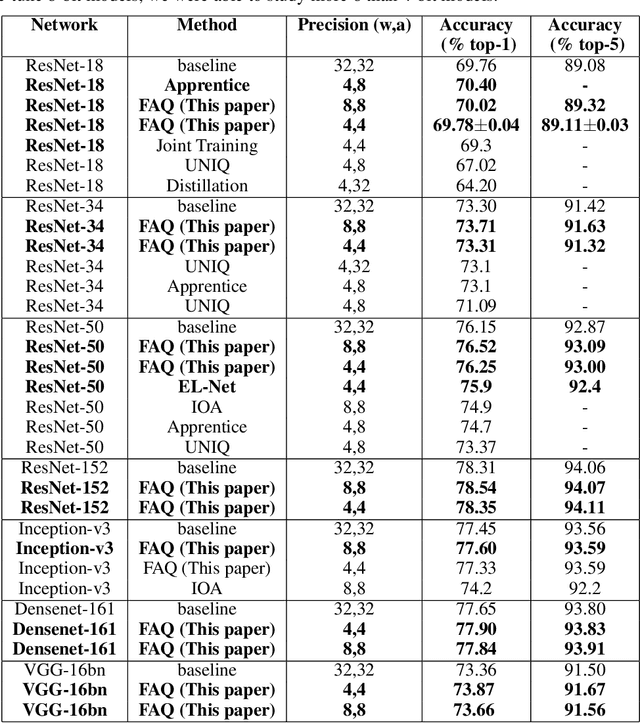
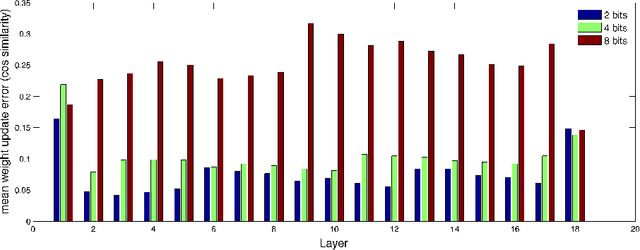
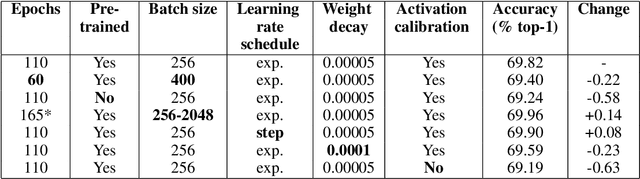
To realize the promise of ubiquitous embedded deep network inference, it is essential to seek limits of energy and area efficiency. To this end, low-precision networks offer tremendous promise because both energy and area scale down quadratically with the reduction in precision. Here, for the first time, we demonstrate ResNet-18, ResNet-34, ResNet-50, ResNet-152, Inception-v3, densenet-161, and VGG-16bn networks on the ImageNet classification benchmark that, at 8-bit precision exceed the accuracy of the full-precision baseline networks after one epoch of finetuning, thereby leveraging the availability of pretrained models. We also demonstrate for the first time ResNet-18, ResNet-34, and ResNet-50 4-bit models that match the accuracy of the full-precision baseline networks. Surprisingly, the weights of the low-precision networks are very close (in cosine similarity) to the weights of the corresponding baseline networks, making training from scratch unnecessary. The number of iterations required by stochastic gradient descent to achieve a given training error is related to the square of (a) the distance of the initial solution from the final plus (b) the maximum variance of the gradient estimates. By drawing inspiration from this observation, we (a) reduce solution distance by starting with pretrained fp32 precision baseline networks and fine-tuning, and (b) combat noise introduced by quantizing weights and activations during training, by using larger batches along with matched learning rate annealing. Together, these two techniques offer a promising heuristic to discover low-precision networks, if they exist, close to fp32 precision baseline networks.