A Fast Power Spectrum Sensing Solution for Generalized Coprime Sampling

The growing scarcity of spectrum resources, wideband spectrum sensing is required to process a prohibitive volume of data at a high sampling rate. For some applications, spectrum estimation only requires second-order statistics. In this case, a fast power spectrum sensing solution is proposed based on the generalized coprime sampling. By exploring the sensing vector inherent structure, the autocorrelation sequence of inputs can be reconstructed from sub-Nyquist samples by only utilizing the parallel Fourier transform and simple multiplication operations. Thus, it takes less time than the state-of-the-art methods while maintaining the same performance, and it achieves higher performance than the existing methods within the same execution time, without the need for pre-estimating the number of inputs. Furthermore, the influence of the model mismatch has only a minor impact on the estimation performance, which allows for more efficient use of the spectrum resource in a distributed swarm scenario. Simulation results demonstrate the low complexity in sampling and computation, making it a more practical solution for real-time and distributed wideband spectrum sensing applications.

Wideband Power Spectrum Sensing: a Fast Practical Solution for Nyquist Folding Receiver

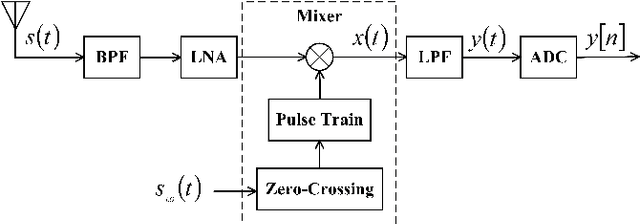
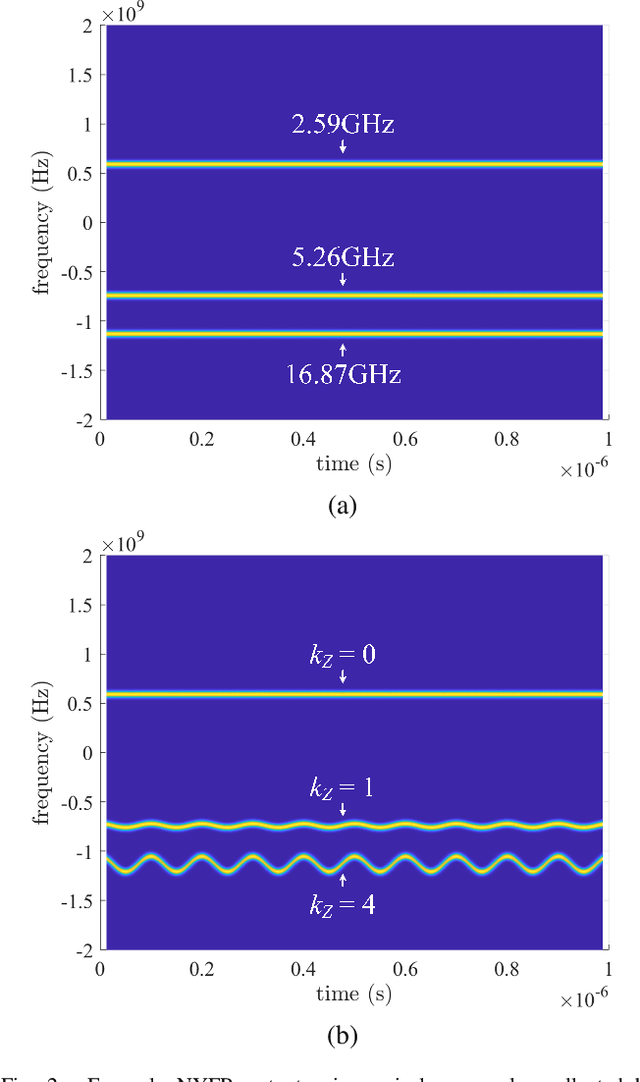
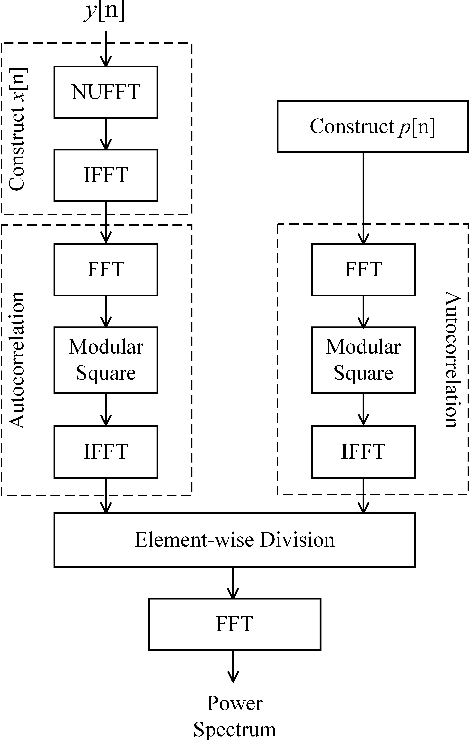
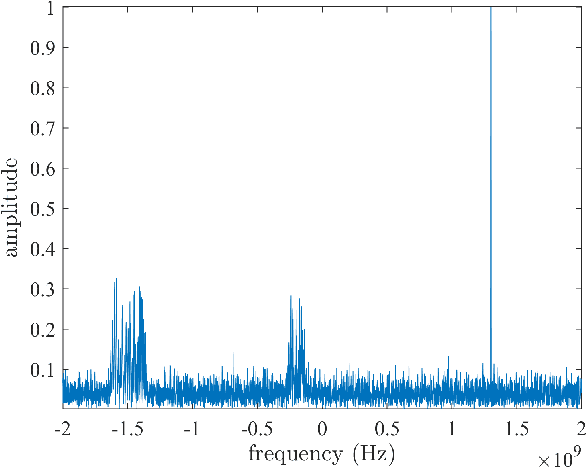
The limited availability of spectrum resources has been growing into a critical problem in wireless communications, remote sensing, and electronic surveillance, etc. To address the high-speed sampling bottleneck of wideband spectrum sensing, a fast and practical solution of power spectrum estimation for Nyquist folding receiver (NYFR) is proposed in this paper. The NYFR architectures is can theoretically achieve the full-band signal sensing with a hundred percent of probability of intercept. But the existing algorithm is difficult to realize in real-time due to its high complexity and complicated calculations. By exploring the sub-sampling principle inherent in NYFR, a computationally efficient method is introduced with compressive covariance sensing. That can be efficient implemented via only the non-uniform fast Fourier transform, fast Fourier transform, and some simple multiplication operations. Meanwhile, the state-of-the-art power spectrum reconstruction model for NYFR of time-domain and frequency-domain is constructed in this paper as a comparison. Furthermore, the computational complexity of the proposed method scales linearly with the Nyquist-rate sampled number of samples and the sparsity of spectrum occupancy. Simulation results and discussion demonstrate that the low complexity in sampling and computation is a more practical solution to meet the real-time wideband spectrum sensing applications.

Distributed UAV Swarm Augmented Wideband Spectrum Sensing Using Nyquist Folding Receiver

Distributed unmanned aerial vehicle (UAV) swarms are formed by multiple UAVs with increased portability, higher levels of sensing capabilities, and more powerful autonomy. These features make them attractive for many recent applica-tions, potentially increasing the shortage of spectrum resources. In this paper, wideband spectrum sensing augmented technology is discussed for distributed UAV swarms to improve the utilization of spectrum. However, the sub-Nyquist sampling applied in existing schemes has high hardware complexity, power consumption, and low recovery efficiency for non-strictly sparse conditions. Thus, the Nyquist folding receiver (NYFR) is considered for the distributed UAV swarms, which can theoretically achieve full-band spectrum detection and reception using a single analog-to-digital converter (ADC) at low speed for all circuit components. There is a focus on the sensing model of two multichannel scenarios for the distributed UAV swarms, one with a complete functional receiver for the UAV swarm with RIS, and another with a decentralized UAV swarm equipped with a complete functional receiver for each UAV element. The key issue is to consider whether the application of RIS technology will bring advantages to spectrum sensing and the data fusion problem of decentralized UAV swarms based on the NYFR architecture. Therefore, the property for multiple pulse reconstruction is analyzed through the Gershgorin circle theorem, especially for very short pulses. Further, the block sparse recovery property is analyzed for wide bandwidth signals. The proposed technology can improve the processing capability for multiple signals and wide bandwidth signals while reducing interference from folded noise and subsampled harmonics. Experiment results show augmented spectrum sensing efficiency under non-strictly sparse conditions.