Dayou Liu
A Survey on Neural-symbolic Systems
Nov 10, 2021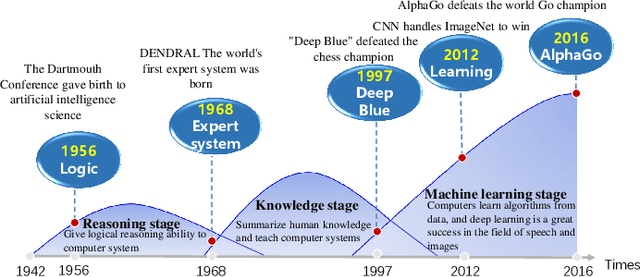
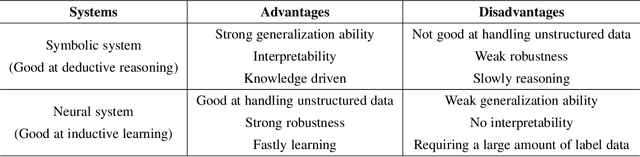
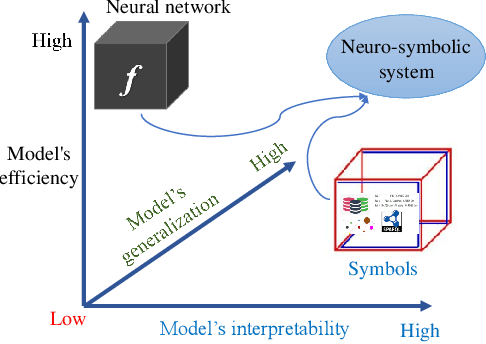
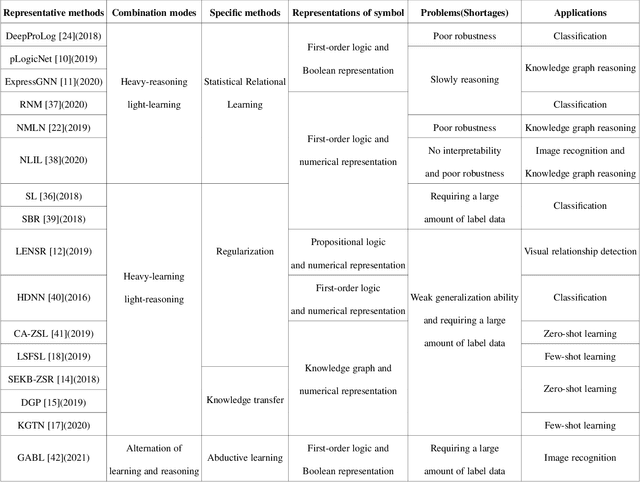
Abstract:In recent years, neural systems have demonstrated superior perceptual intelligence through highly effective learning, but their reasoning capabilities remain poor. In contrast, symbolic systems have exceptional cognitive intelligence through efficient reasoning, but their learning capabilities are poor. In this case, an ideal intelligent system--a neural-symbolic system--with high perceptual and cognitive intelligence through powerful learning and reasoning capabilities gains a growing interest in the research community. Combining the fast computation ability of neural systems and the powerful expression ability of symbolic systems, neural-symbolic systems can perform effective learning and reasoning in multi-domain tasks, demonstrating concurrent perception and cognition capabilities in intelligent systems. This paper surveys the latest research in neural-symbolic systems along four dimensions: the necessity of combination, technical challenges, methods, and applications. This paper aims to help advance this emerging area of research by providing researchers with a holistic and comprehensive view, highlighting the state of art and identifying the opportunities.
Ordered {AND, OR}-Decomposition and Binary-Decision Diagram
Oct 27, 2014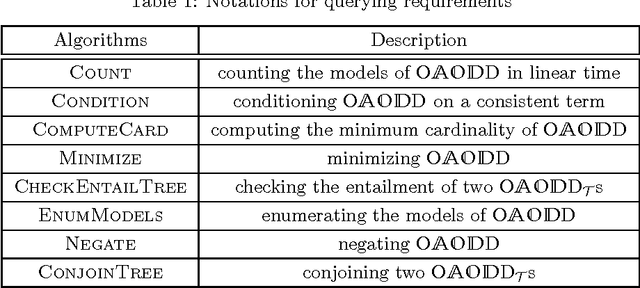
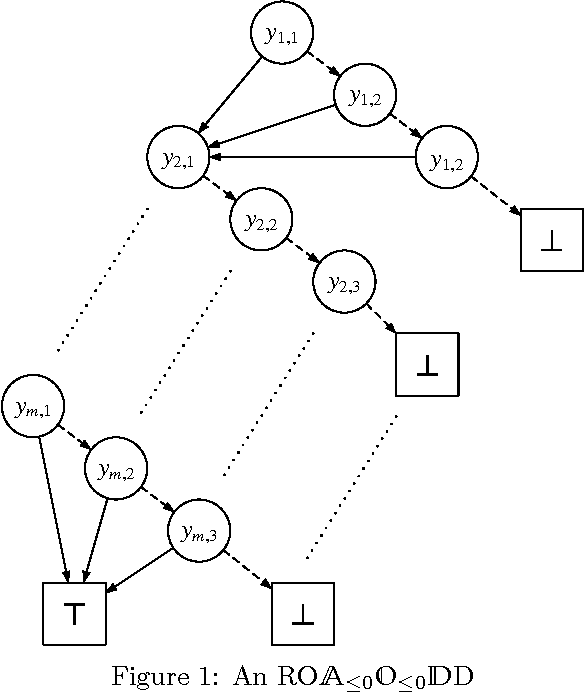
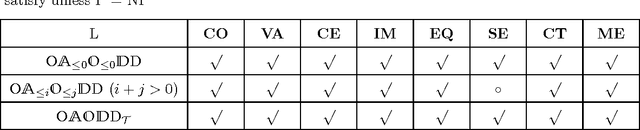
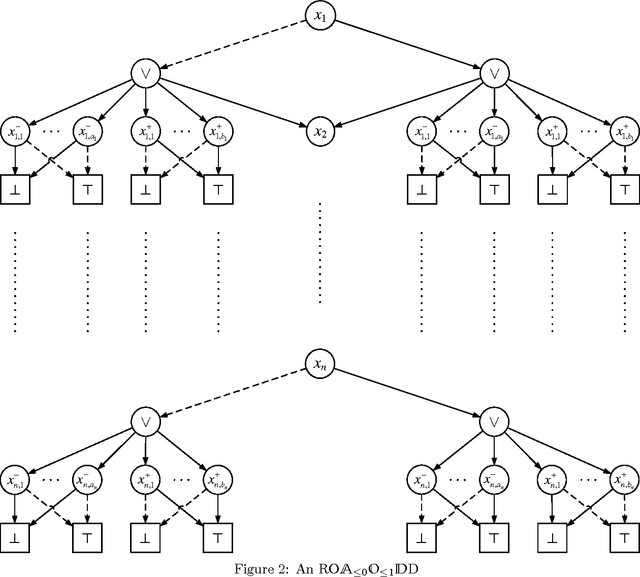
Abstract:In the context of knowledge compilation (KC), we study the effect of augmenting Ordered Binary Decision Diagrams (OBDD) with two kinds of decomposition nodes, i.e., AND-vertices and OR-vertices which denote conjunctive and disjunctive decomposition of propositional knowledge bases, respectively. The resulting knowledge compilation language is called Ordered {AND, OR}-decomposition and binary-Decision Diagram (OAODD). Roughly speaking, several previous languages can be seen as special types of OAODD, including OBDD, AND/OR Binary Decision Diagram (AOBDD), OBDD with implied Literals (OBDD-L), Multi-Level Decomposition Diagrams (MLDD). On the one hand, we propose some families of algorithms which can convert some fragments of OAODD into others; on the other hand, we present a rich set of polynomial-time algorithms that perform logical operations. According to these algorithms, as well as theoretical analysis, we characterize the space efficiency and tractability of OAODD and its some fragments with respect to the evaluating criteria in the KC map. Finally, we present a compilation algorithm which can convert formulas in negative normal form into OAODD.
Augmenting Ordered Binary Decision Diagrams with Conjunctive Decomposition
Oct 24, 2014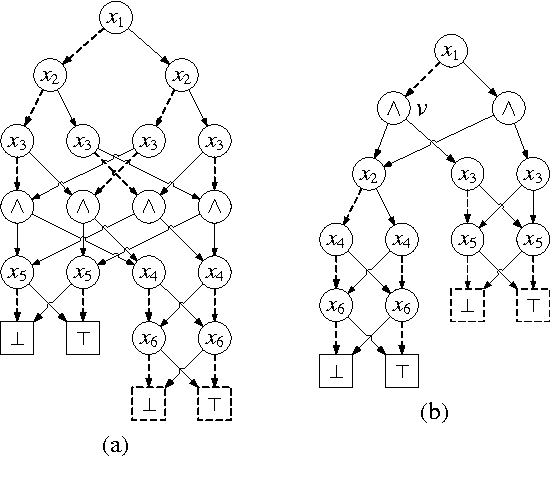
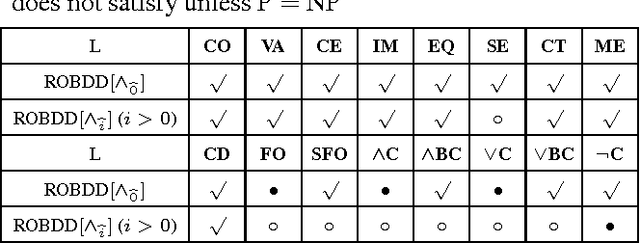

Abstract:This paper augments OBDD with conjunctive decomposition to propose a generalization called OBDD[$\wedge$]. By imposing reducedness and the finest $\wedge$-decomposition bounded by integer $i$ ($\wedge_{\widehat{i}}$-decomposition) on OBDD[$\wedge$], we identify a family of canonical languages called ROBDD[$\wedge_{\widehat{i}}$], where ROBDD[$\wedge_{\widehat{0}}$] is equivalent to ROBDD. We show that the succinctness of ROBDD[$\wedge_{\widehat{i}}$] is strictly increasing when $i$ increases. We introduce a new time-efficiency criterion called rapidity which reflects that exponential operations may be preferable if the language can be exponentially more succinct, and show that: the rapidity of each operation on ROBDD[$\wedge_{\widehat{i}}$] is increasing when $i$ increases; particularly, the rapidity of some operations (e.g., conjoining) is strictly increasing. Finally, our empirical results show that: a) the size of ROBDD[$\wedge_{\widehat{i}}$] is normally not larger than that of the equivalent \ROBDDC{\widehat{i+1}}; b) conjoining two ROBDD[$\wedge_{\widehat{1}}$]s is more efficient than conjoining two ROBDD[$\wedge_{\widehat{0}}$]s in most cases, where the former is NP-hard but the latter is in P; and c) the space-efficiency of ROBDD[$\wedge_{\widehat{\infty}}$] is comparable with that of d-DNNF and that of another canonical generalization of \ROBDD{} called SDD.
Reduced Ordered Binary Decision Diagram with Implied Literals: A New knowledge Compilation Approach
Mar 24, 2011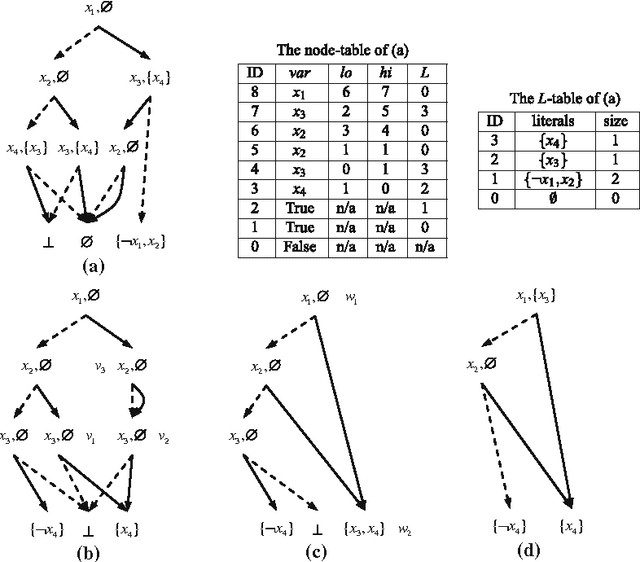

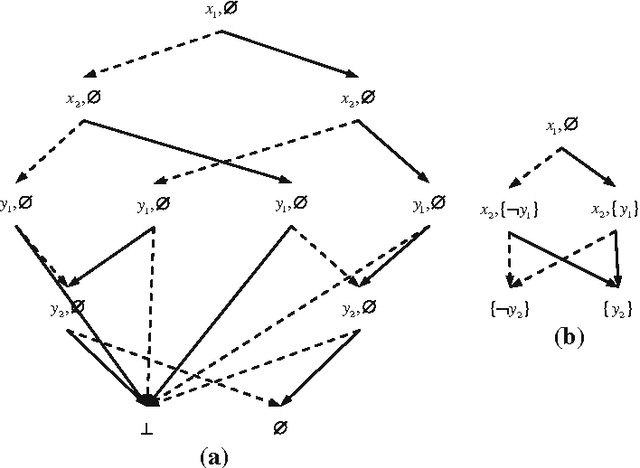
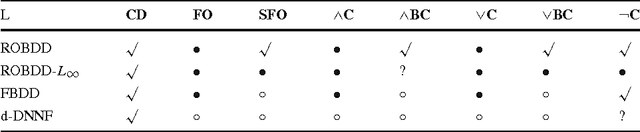
Abstract:Knowledge compilation is an approach to tackle the computational intractability of general reasoning problems. According to this approach, knowledge bases are converted off-line into a target compilation language which is tractable for on-line querying. Reduced ordered binary decision diagram (ROBDD) is one of the most influential target languages. We generalize ROBDD by associating some implied literals in each node and the new language is called reduced ordered binary decision diagram with implied literals (ROBDD-L). Then we discuss a kind of subsets of ROBDD-L called ROBDD-i with precisely i implied literals (0 \leq i \leq \infty). In particular, ROBDD-0 is isomorphic to ROBDD; ROBDD-\infty requires that each node should be associated by the implied literals as many as possible. We show that ROBDD-i has uniqueness over some specific variables order, and ROBDD-\infty is the most succinct subset in ROBDD-L and can meet most of the querying requirements involved in the knowledge compilation map. Finally, we propose an ROBDD-i compilation algorithm for any i and a ROBDD-\infty compilation algorithm. Based on them, we implement a ROBDD-L package called BDDjLu and then get some conclusions from preliminary experimental results: ROBDD-\infty is obviously smaller than ROBDD for all benchmarks; ROBDD-\infty is smaller than the d-DNNF the benchmarks whose compilation results are relatively small; it seems that it is better to transform ROBDDs-\infty into FBDDs and ROBDDs rather than straight compile the benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge