Augmenting Ordered Binary Decision Diagrams with Conjunctive Decomposition
Paper and Code
Oct 24, 2014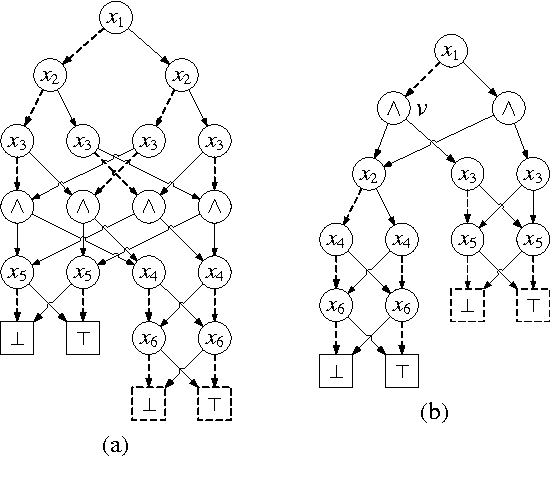
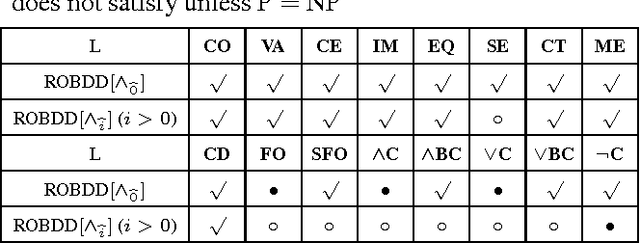

This paper augments OBDD with conjunctive decomposition to propose a generalization called OBDD[$\wedge$]. By imposing reducedness and the finest $\wedge$-decomposition bounded by integer $i$ ($\wedge_{\widehat{i}}$-decomposition) on OBDD[$\wedge$], we identify a family of canonical languages called ROBDD[$\wedge_{\widehat{i}}$], where ROBDD[$\wedge_{\widehat{0}}$] is equivalent to ROBDD. We show that the succinctness of ROBDD[$\wedge_{\widehat{i}}$] is strictly increasing when $i$ increases. We introduce a new time-efficiency criterion called rapidity which reflects that exponential operations may be preferable if the language can be exponentially more succinct, and show that: the rapidity of each operation on ROBDD[$\wedge_{\widehat{i}}$] is increasing when $i$ increases; particularly, the rapidity of some operations (e.g., conjoining) is strictly increasing. Finally, our empirical results show that: a) the size of ROBDD[$\wedge_{\widehat{i}}$] is normally not larger than that of the equivalent \ROBDDC{\widehat{i+1}}; b) conjoining two ROBDD[$\wedge_{\widehat{1}}$]s is more efficient than conjoining two ROBDD[$\wedge_{\widehat{0}}$]s in most cases, where the former is NP-hard but the latter is in P; and c) the space-efficiency of ROBDD[$\wedge_{\widehat{\infty}}$] is comparable with that of d-DNNF and that of another canonical generalization of \ROBDD{} called SDD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge