Analysis and Design of Convolutional Networks via Hierarchical Tensor Decompositions

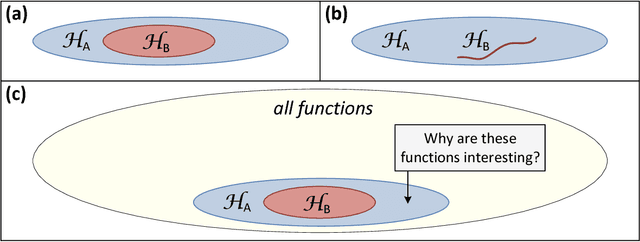
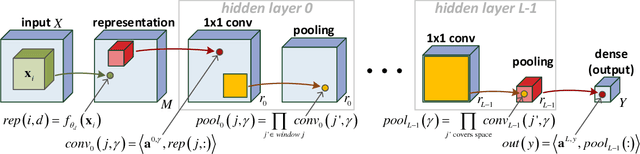
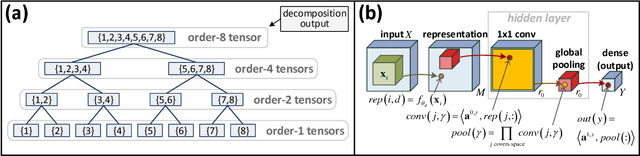
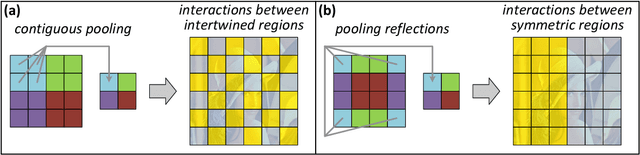
The driving force behind convolutional networks - the most successful deep learning architecture to date, is their expressive power. Despite its wide acceptance and vast empirical evidence, formal analyses supporting this belief are scarce. The primary notions for formally reasoning about expressiveness are efficiency and inductive bias. Expressive efficiency refers to the ability of a network architecture to realize functions that require an alternative architecture to be much larger. Inductive bias refers to the prioritization of some functions over others given prior knowledge regarding a task at hand. In this paper we overview a series of works written by the authors, that through an equivalence to hierarchical tensor decompositions, analyze the expressive efficiency and inductive bias of various convolutional network architectural features (depth, width, strides and more). The results presented shed light on the demonstrated effectiveness of convolutional networks, and in addition, provide new tools for network design.

Deep Learning and Quantum Entanglement: Fundamental Connections with Implications to Network Design

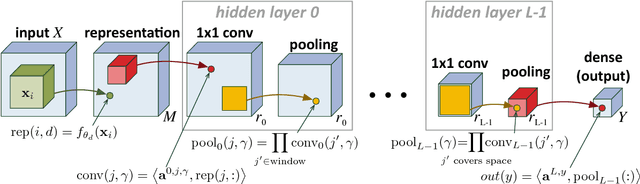
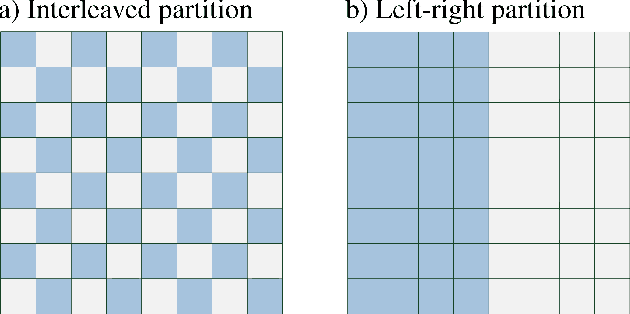
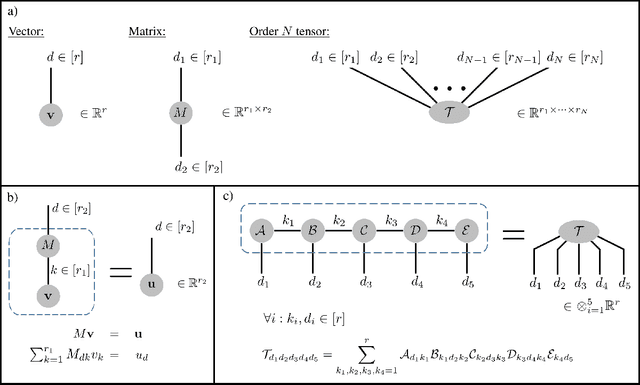
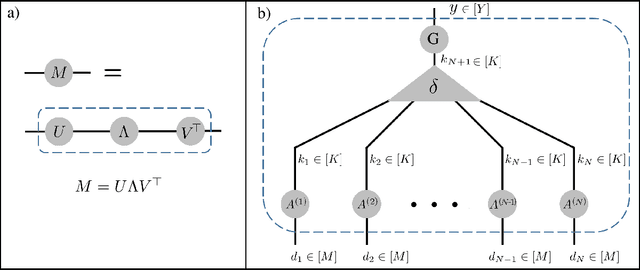
Deep convolutional networks have witnessed unprecedented success in various machine learning applications. Formal understanding on what makes these networks so successful is gradually unfolding, but for the most part there are still significant mysteries to unravel. The inductive bias, which reflects prior knowledge embedded in the network architecture, is one of them. In this work, we establish a fundamental connection between the fields of quantum physics and deep learning. We use this connection for asserting novel theoretical observations regarding the role that the number of channels in each layer of the convolutional network fulfills in the overall inductive bias. Specifically, we show an equivalence between the function realized by a deep convolutional arithmetic circuit (ConvAC) and a quantum many-body wave function, which relies on their common underlying tensorial structure. This facilitates the use of quantum entanglement measures as well-defined quantifiers of a deep network's expressive ability to model intricate correlation structures of its inputs. Most importantly, the construction of a deep ConvAC in terms of a Tensor Network is made available. This description enables us to carry a graph-theoretic analysis of a convolutional network, with which we demonstrate a direct control over the inductive bias of the deep network via its channel numbers, that are related to the min-cut in the underlying graph. This result is relevant to any practitioner designing a network for a specific task. We theoretically analyze ConvACs, and empirically validate our findings on more common ConvNets which involve ReLU activations and max pooling. Beyond the results described above, the description of a deep convolutional network in well-defined graph-theoretic tools and the formal connection to quantum entanglement, are two interdisciplinary bridges that are brought forth by this work.