Calibration tests in multi-class classification: A unifying framework

In safety-critical applications a probabilistic model is usually required to be calibrated, i.e., to capture the uncertainty of its predictions accurately. In multi-class classification, calibration of the most confident predictions only is often not sufficient. We propose and study calibration measures for multi-class classification that generalize existing measures such as the expected calibration error, the maximum calibration error, and the maximum mean calibration error. We propose and evaluate empirically different consistent and unbiased estimators for a specific class of measures based on matrix-valued kernels. Importantly, these estimators can be interpreted as test statistics associated with well-defined bounds and approximations of the p-value under the null hypothesis that the model is calibrated, significantly improving the interpretability of calibration measures, which otherwise lack any meaningful unit or scale.

Evaluating model calibration in classification

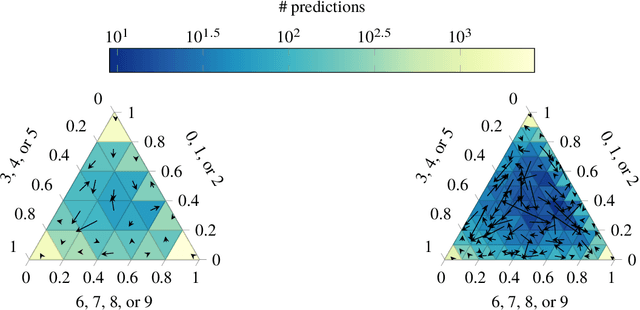
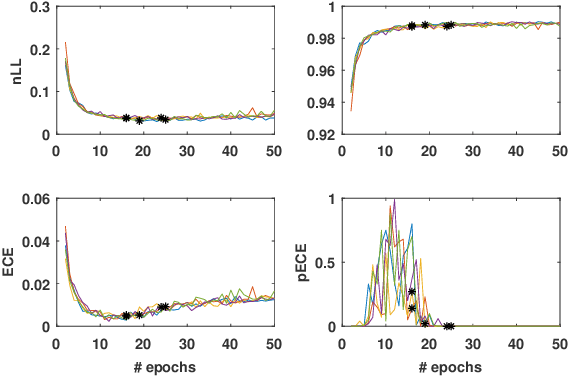
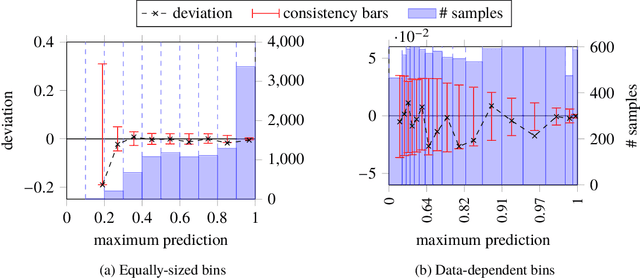
Probabilistic classifiers output a probability distribution on target classes rather than just a class prediction. Besides providing a clear separation of prediction and decision making, the main advantage of probabilistic models is their ability to represent uncertainty about predictions. In safety-critical applications, it is pivotal for a model to possess an adequate sense of uncertainty, which for probabilistic classifiers translates into outputting probability distributions that are consistent with the empirical frequencies observed from realized outcomes. A classifier with such a property is called calibrated. In this work, we develop a general theoretical calibration evaluation framework grounded in probability theory, and point out subtleties present in model calibration evaluation that lead to refined interpretations of existing evaluation techniques. Lastly, we propose new ways to quantify and visualize miscalibration in probabilistic classification, including novel multidimensional reliability diagrams.