Methods for pitch analysis in contemporary popular music: Vitalic's use of tones that do not operate on the principle of acoustic resonance

Vitalic is an electronic music producer who has been active since 2001. Vitalic's 2005 track "No Fun" features a main synthesiser part built from a sequence of single inharmonic tones that evoke two simultaneous melodies. This part serves as a starting point for examining Vitalic's use of tones that do not operate on the principle of acoustic resonance. The study considers tones that evoke two or more simultaneous pitches and examines various inharmonic partial layouts. Examples outside Vitalic's music are also provided to suggest that similar tone properties can be found elsewhere in contemporary popular music.

Wavelet-Filtering of Symbolic Music Representations for Folk Tune Segmentation and Classification

The aim of this study is to evaluate a machine-learning method in which symbolic representations of folk songs are segmented and classified into tune families with Haar-wavelet filtering. The method is compared with previously proposed Gestalt-based method. Melodies are represented as discrete symbolic pitch-time signals. We apply the continuous wavelet transform (CWT) with the Haar wavelet at specific scales, obtaining filtered versions of melodies emphasizing their information at particular time-scales. We use the filtered signal for representation and segmentation, using the wavelet coefficients' local maxima to indicate local boundaries and classify segments by means of k-nearest neighbours based on standard vector-metrics (Euclidean, cityblock), and compare the results to a Gestalt-based segmentation method and metrics applied directly to the pitch signal. We found that the wavelet based segmentation and wavelet-filtering of the pitch signal lead to better classification accuracy in cross-validated evaluation when the time-scale and other parameters are optimized.

An approach to melodic segmentation and classification based on filtering with the Haar-wavelet

We present a novel method of classification and segmentation of melodies in symbolic representation. The method is based on filtering pitch as a signal over time with the Haar-wavelet, and we evaluate it on two tasks. The filtered signal corresponds to a single-scale signal ws from the continuous Haar wavelet transform. The melodies are first segmented using local maxima or zero-crossings of w_s. The segments of w_s are then classified using the k-nearest neighbour algorithm with Euclidian and city-block distances. The method proves more effective than using unfiltered pitch signals and Gestalt-based segmentation when used to recognize the parent works of segments from Bach's Two-Part Inventions (BWV 772-786). When used to classify 360 Dutch folk tunes into 26 tune families, the performance of the method is comparable to the use of pitch signals, but not as good as that of string-matching methods based on multiple features.

The evolution of inharmonicity and noisiness in contemporary popular music

Much of Western classical music uses instruments based on acoustic resonance. Such instruments produce harmonic or quasi-harmonic sounds. On the other hand, since the early 1970s, popular music has largely been produced in the recording studio. As a result, popular music is not bound to be based on harmonic or quasi-harmonic sounds. In this study, we use modified MPEG-7 features to explore and characterise the way in which the use of noise and inharmonicity has evolved in popular music since 1961. We set this evolution in the context of other broad categories of music, including Western classical piano music, Western classical orchestral music, and musique concr\`ete. We propose new features that allow us to distinguish between inharmonicity resulting from noise and inharmonicity resulting from interactions between relatively discrete partials. When the history of contemporary popular music is viewed through the lens of these new features, we find that the period since 1961 can be divided into three phases. From 1961 to 1972, there was a steady increase in inharmonicity but no significant increase in noise. From 1972 to 1986, both inharmonicity and noise increased. Then, since 1986, there has been a steady decrease in both inharmonicity and noise to today's popular music which is significantly less noisy but more inharmonic than the music of the sixties. We relate these observed trends to the development of music production practice over the period and illustrate them with focused analyses of certain key artists and tracks.

Understanding and Compressing Music with Maximal Transformable Patterns

We present a polynomial-time algorithm that discovers all maximal patterns in a point set, $D\subset\mathbb{R}^k$, that are related by transformations in a user-specified class, $F$, of bijections over $\mathbb{R}^k$. We also present a second algorithm that discovers the set of occurrences for each of these maximal patterns and then uses compact encodings of these occurrence sets to compute a losslessly compressed encoding of the input point set. This encoding takes the form of a set of pairs, $E=\left\lbrace\left\langle P_1, T_1\right\rangle,\left\langle P_2, T_2\right\rangle,\ldots\left\langle P_{\ell}, T_{\ell}\right\rangle\right\rbrace$, where each $\langle P_i,T_i\rangle$ consists of a maximal pattern, $P_i\subseteq D$, and a set, $T_i\subset F$, of transformations that map $P_i$ onto other subsets of $D$. Each transformation is encoded by a vector of real values that uniquely identifies it within $F$ and the length of this vector is used as a measure of the complexity of $F$. We evaluate the new compression algorithm with three transformation classes of differing complexity, on the task of classifying folk-song melodies into tune families. The most complex of the classes tested includes all combinations of the musical transformations of transposition, inversion, retrograde, augmentation and diminution. We found that broadening the transformation class improved performance on this task. However, it did not, on average, improve compression factor, which may be due to the datasets (in this case, folk-song melodies) being too short and simple to benefit from the potentially greater number of pattern relationships that are discoverable with larger transformation classes.

RECURSIA-RRT: Recursive translatable point-set pattern discovery with removal of redundant translators

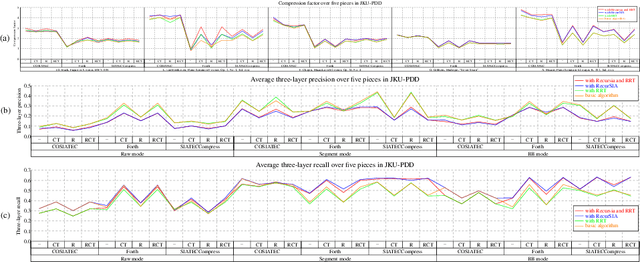
Two algorithms, RECURSIA and RRT, are presented, designed to increase the compression factor achieved using SIATEC-based point-set cover algorithms. RECURSIA recursively applies a TEC cover algorithm to the patterns in the TECs that it discovers. RRT attempts to remove translators from each TEC without reducing its covered set. When evaluated with COSIATEC, SIATECCompress and Forth's algorithm on the JKU Patterns Development Database, using RECURSIA with or without RRT increased compression factor and recall but reduced precision. Using RRT alone increased compression factor and reduced recall and precision, but had a smaller effect than RECURSIA.