Maximum entropy and quantized metric models for absolute category ratings

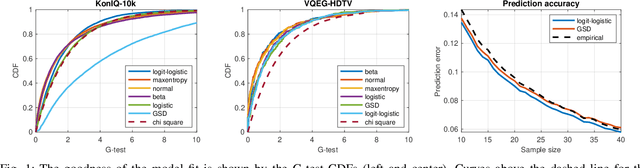
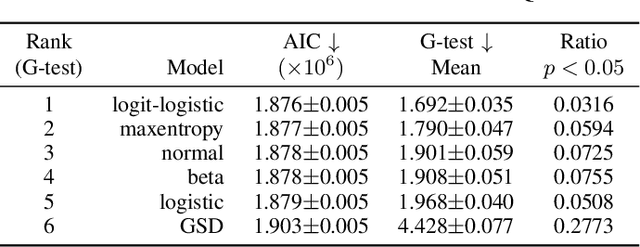
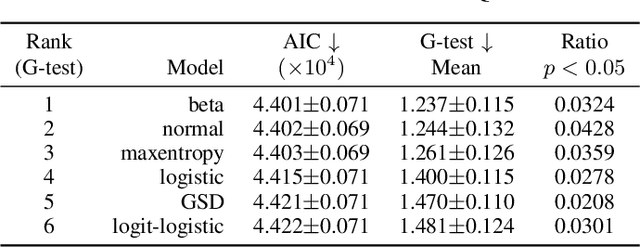
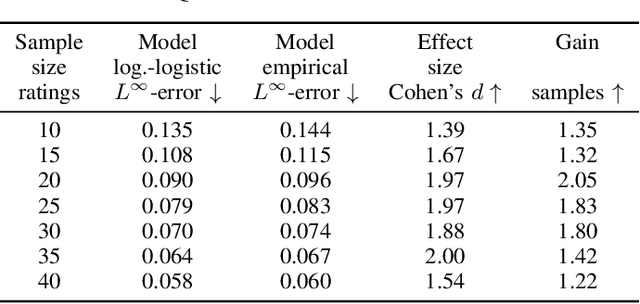
The datasets of most image quality assessment studies contain ratings on a categorical scale with five levels, from bad (1) to excellent (5). For each stimulus, the number of ratings from 1 to 5 is summarized and given in the form of the mean opinion score. In this study, we investigate families of multinomial probability distributions parameterized by mean and variance that are used to fit the empirical rating distributions. To this end, we consider quantized metric models based on continuous distributions that model perceived stimulus quality on a latent scale. The probabilities for the rating categories are determined by quantizing the corresponding random variables using threshold values. Furthermore, we introduce a novel discrete maximum entropy distribution for a given mean and variance. We compare the performance of these models and the state of the art given by the generalized score distribution for two large data sets, KonIQ-10k and VQEG HDTV. Given an input distribution of ratings, our fitted two-parameter models predict unseen ratings better than the empirical distribution. In contrast to empirical ACR distributions and their discrete models, our continuous models can provide fine-grained estimates of quantiles of quality of experience that are relevant to service providers to satisfy a target fraction of the user population.

Out-of-Core Dimensionality Reduction for Large Data via Out-of-Sample Extensions

Dimensionality reduction (DR) is a well-established approach for the visualization of high-dimensional data sets. While DR methods are often applied to typical DR benchmark data sets in the literature, they might suffer from high runtime complexity and memory requirements, making them unsuitable for large data visualization especially in environments outside of high-performance computing. To perform DR on large data sets, we propose the use of out-of-sample extensions. Such extensions allow inserting new data into existing projections, which we leverage to iteratively project data into a reference projection that consists only of a small manageable subset. This process makes it possible to perform DR out-of-core on large data, which would otherwise not be possible due to memory and runtime limitations. For metric multidimensional scaling (MDS), we contribute an implementation with out-of-sample projection capability since typical software libraries do not support it. We provide an evaluation of the projection quality of five common DR algorithms (MDS, PCA, t-SNE, UMAP, and autoencoders) using quality metrics from the literature and analyze the trade-off between the size of the reference set and projection quality. The runtime behavior of the algorithms is also quantified with respect to reference set size, out-of-sample batch size, and dimensionality of the data sets. Furthermore, we compare the out-of-sample approach to other recently introduced DR methods, such as PaCMAP and TriMAP, which claim to handle larger data sets than traditional approaches. To showcase the usefulness of DR on this large scale, we contribute a use case where we analyze ensembles of streamlines amounting to one billion projected instances.

Visualization of Nonlinear Programming for Robot Motion Planning

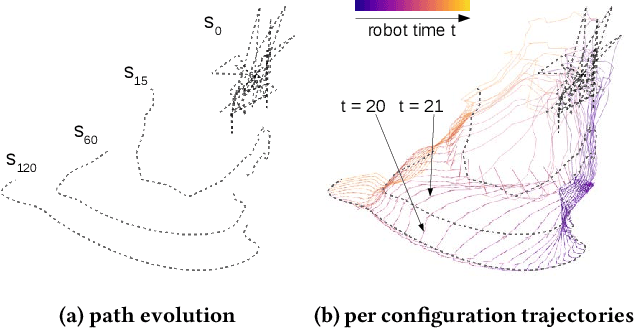
Nonlinear programming targets nonlinear optimization with constraints, which is a generic yet complex methodology involving humans for problem modeling and algorithms for problem solving. We address the particularly hard challenge of supporting domain experts in handling, understanding, and trouble-shooting high-dimensional optimization with a large number of constraints. Leveraging visual analytics, users are supported in exploring the computation process of nonlinear constraint optimization. Our system was designed for robot motion planning problems and developed in tight collaboration with domain experts in nonlinear programming and robotics. We report on the experiences from this design study, illustrate the usefulness for relevant example cases, and discuss the extension to visual analytics for nonlinear programming in general.