The Parallel Algorithm for the 2-D Discrete Wavelet Transform

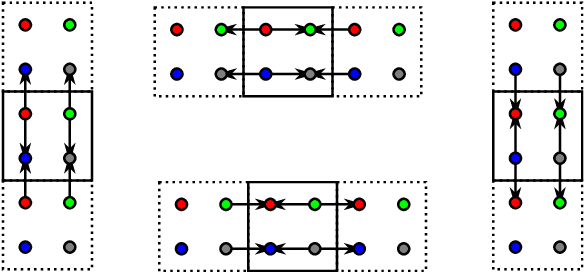
The discrete wavelet transform can be found at the heart of many image-processing algorithms. Until now, the transform on general-purpose processors (CPUs) was mostly computed using a separable lifting scheme. As the lifting scheme consists of a small number of operations, it is preferred for processing using single-core CPUs. However, considering a parallel processing using multi-core processors, this scheme is inappropriate due to a large number of steps. On such architectures, the number of steps corresponds to the number of points that represent the exchange of data. Consequently, these points often form a performance bottleneck. Our approach appropriately rearranges calculations inside the transform, and thereby reduces the number of steps. In other words, we propose a new scheme that is friendly to parallel environments. When evaluating on multi-core CPUs, we consistently overcome the original lifting scheme. The evaluation was performed on 61-core Intel Xeon Phi and 8-core Intel Xeon processors.

Accelerating Discrete Wavelet Transforms on GPUs

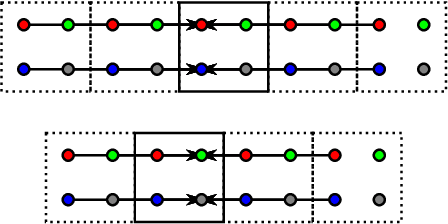
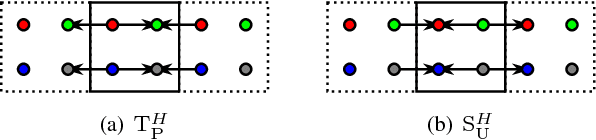
The two-dimensional discrete wavelet transform has a huge number of applications in image-processing techniques. Until now, several papers compared the performance of such transform on graphics processing units (GPUs). However, all of them only dealt with lifting and convolution computation schemes. In this paper, we show that corresponding horizontal and vertical lifting parts of the lifting scheme can be merged into non-separable lifting units, which halves the number of steps. We also discuss an optimization strategy leading to a reduction in the number of arithmetic operations. The schemes were assessed using the OpenCL and pixel shaders. The proposed non-separable lifting scheme outperforms the existing schemes in many cases, irrespective of its higher complexity.

Parallel Wavelet Schemes for Images

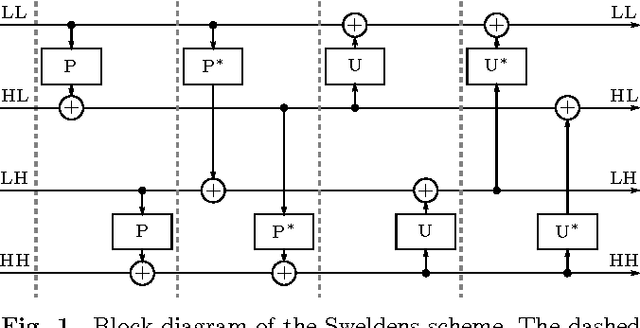
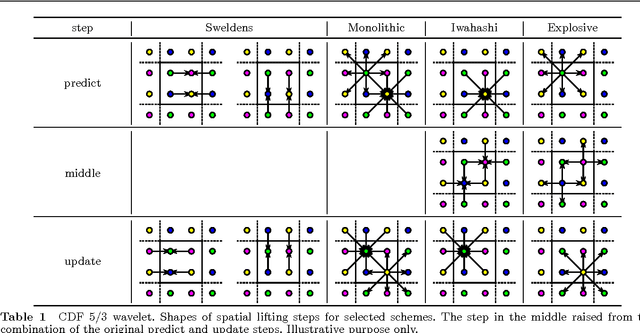
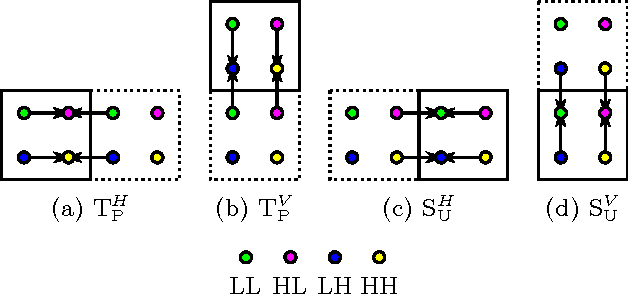
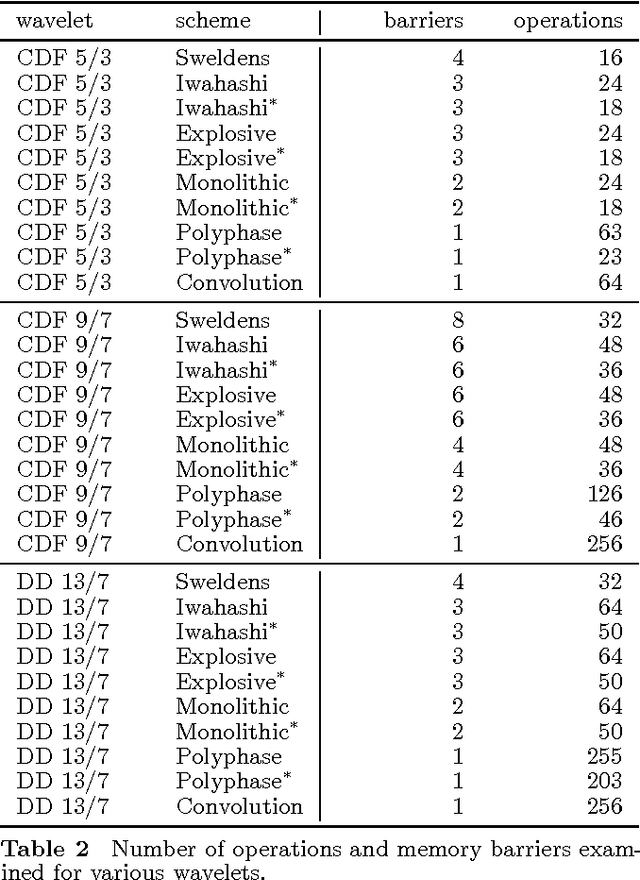
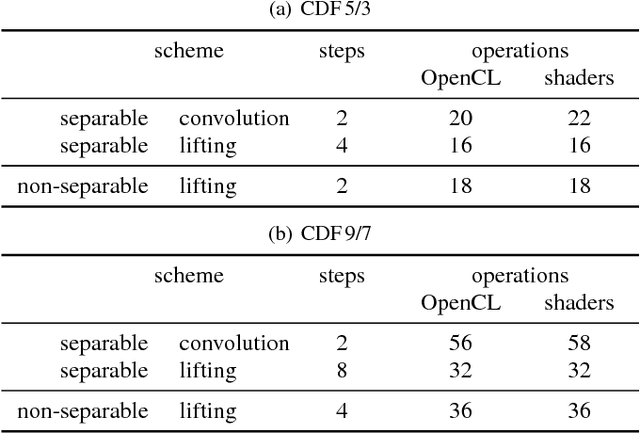
In this paper, we introduce several new schemes for calculation of discrete wavelet transforms of images. These schemes reduce the number of steps and, as a consequence, allow to reduce the number of synchronizations on parallel architectures. As an additional useful property, the proposed schemes can reduce also the number of arithmetic operations. The schemes are primarily demonstrated on CDF 5/3 and CDF 9/7 wavelets employed in JPEG 2000 image compression standard. However, the presented method is general, and it can be applied on any wavelet transform. As a result, our scheme requires only two memory barriers for 2-D CDF 5/3 transform compared to four barriers in the original separable form or three barriers in the non-separable scheme recently published. Our reasoning is supported by exhaustive experiments on high-end graphics cards.

Compression Artifacts Removal Using Convolutional Neural Networks

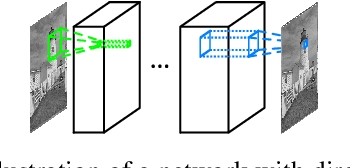
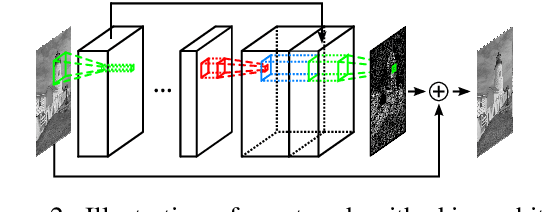
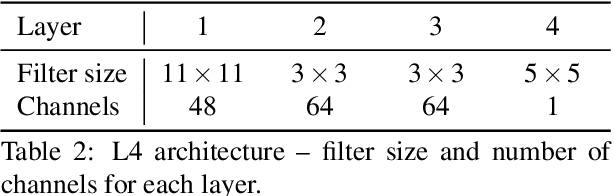
This paper shows that it is possible to train large and deep convolutional neural networks (CNN) for JPEG compression artifacts reduction, and that such networks can provide significantly better reconstruction quality compared to previously used smaller networks as well as to any other state-of-the-art methods. We were able to train networks with 8 layers in a single step and in relatively short time by combining residual learning, skip architecture, and symmetric weight initialization. We provide further insights into convolution networks for JPEG artifact reduction by evaluating three different objectives, generalization with respect to training dataset size, and generalization with respect to JPEG quality level.

Gabor Wavelets in Image Processing

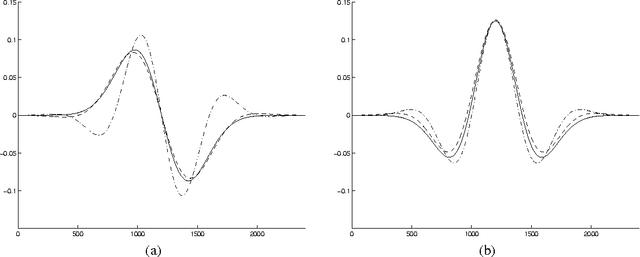
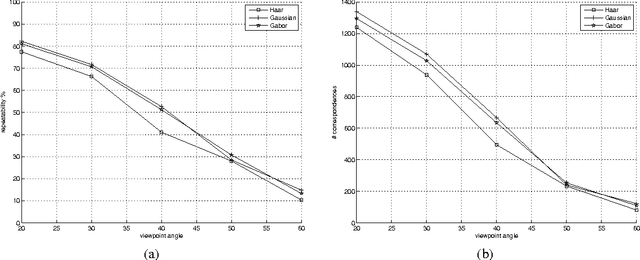
This work shows the use of a two-dimensional Gabor wavelets in image processing. Convolution with such a two-dimensional wavelet can be separated into two series of one-dimensional ones. The key idea of this work is to utilize a Gabor wavelet as a multiscale partial differential operator of a given order. Gabor wavelets are used here to detect edges, corners and blobs. A performance of such an interest point detector is compared to detectors utilizing a Haar wavelet and a derivative of a Gaussian function. The proposed approach may be useful when a fast implementation of the Gabor transform is available or when the transform is already precomputed.