Gabor Wavelets in Image Processing
Paper and Code
Feb 10, 2016
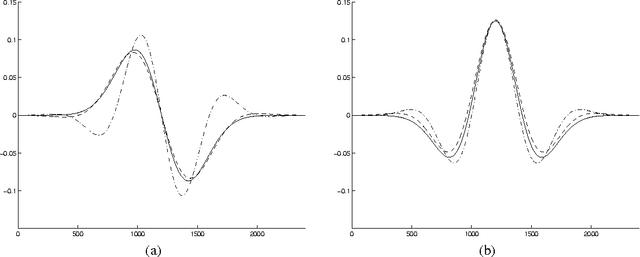

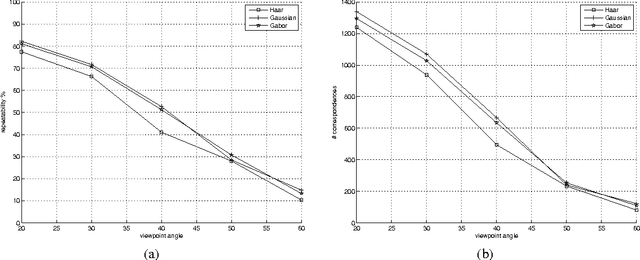
This work shows the use of a two-dimensional Gabor wavelets in image processing. Convolution with such a two-dimensional wavelet can be separated into two series of one-dimensional ones. The key idea of this work is to utilize a Gabor wavelet as a multiscale partial differential operator of a given order. Gabor wavelets are used here to detect edges, corners and blobs. A performance of such an interest point detector is compared to detectors utilizing a Haar wavelet and a derivative of a Gaussian function. The proposed approach may be useful when a fast implementation of the Gabor transform is available or when the transform is already precomputed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge