Parallel Wavelet Schemes for Images
Paper and Code
Oct 12, 2016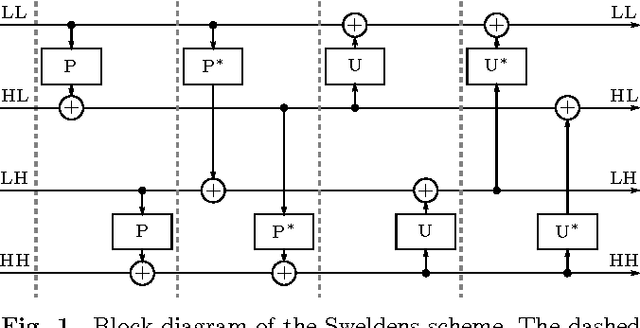
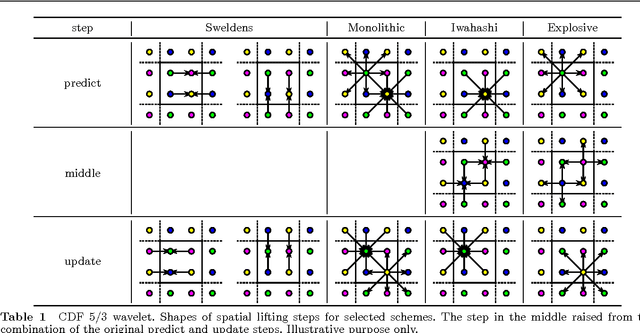
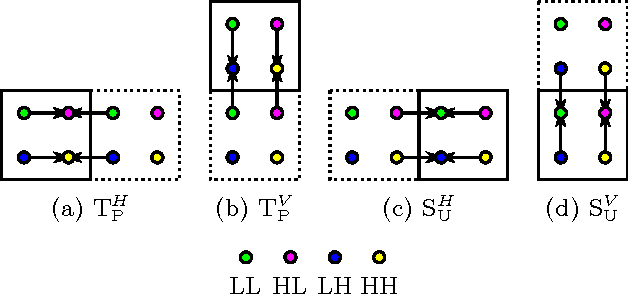
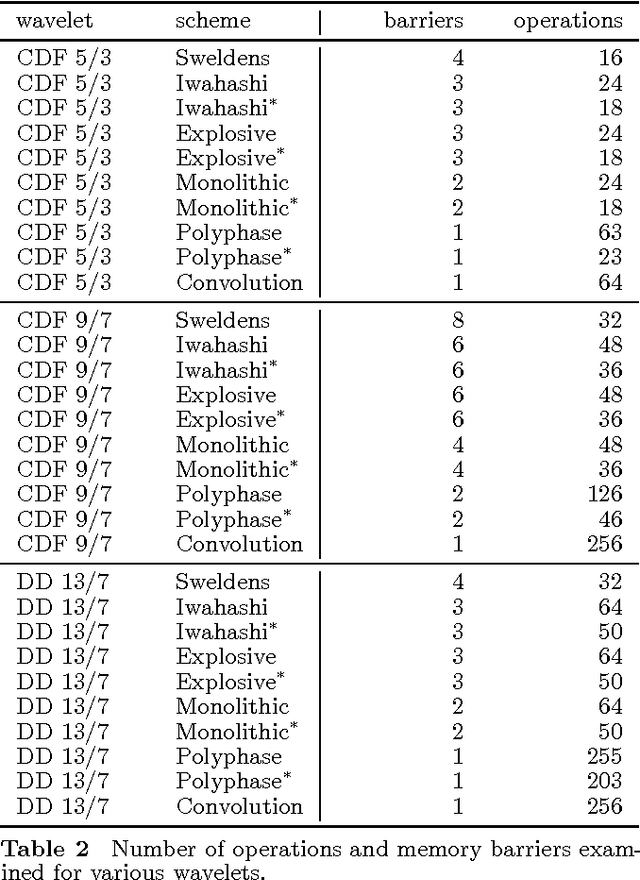
In this paper, we introduce several new schemes for calculation of discrete wavelet transforms of images. These schemes reduce the number of steps and, as a consequence, allow to reduce the number of synchronizations on parallel architectures. As an additional useful property, the proposed schemes can reduce also the number of arithmetic operations. The schemes are primarily demonstrated on CDF 5/3 and CDF 9/7 wavelets employed in JPEG 2000 image compression standard. However, the presented method is general, and it can be applied on any wavelet transform. As a result, our scheme requires only two memory barriers for 2-D CDF 5/3 transform compared to four barriers in the original separable form or three barriers in the non-separable scheme recently published. Our reasoning is supported by exhaustive experiments on high-end graphics cards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge