Inferring Manifolds From Noisy Data Using Gaussian Processes

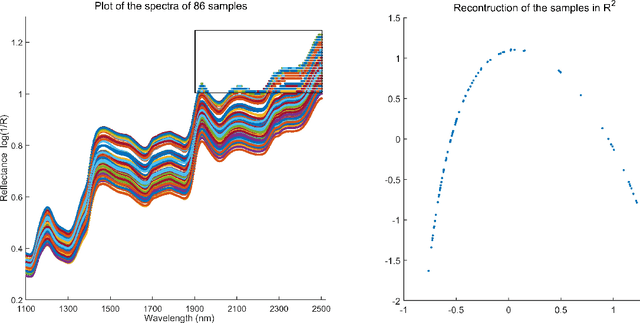
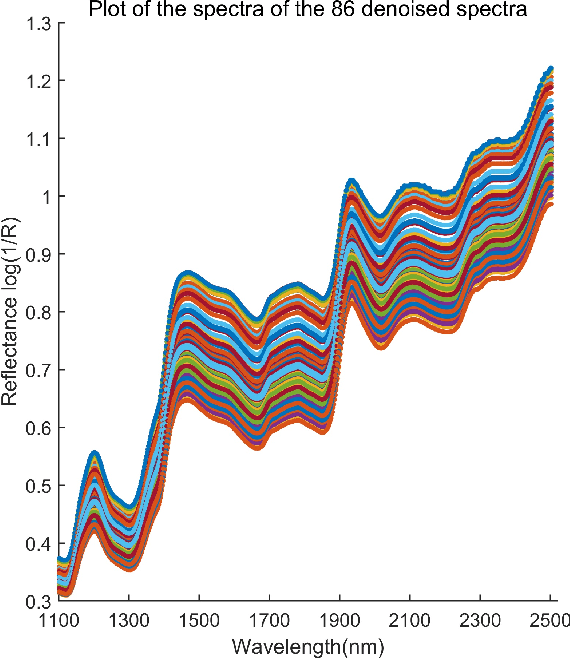
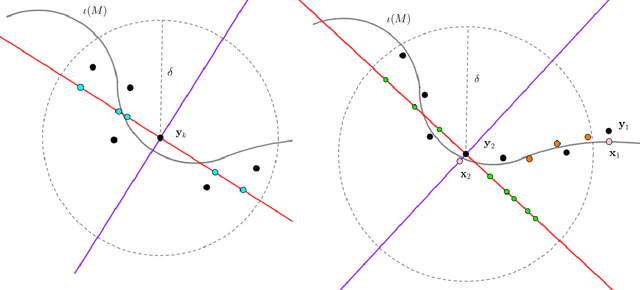
In analyzing complex datasets, it is often of interest to infer lower dimensional structure underlying the higher dimensional observations. As a flexible class of nonlinear structures, it is common to focus on Riemannian manifolds. Most existing manifold learning algorithms replace the original data with lower dimensional coordinates without providing an estimate of the manifold in the observation space or using the manifold to denoise the original data. This article proposes a new methodology for addressing these problems, allowing interpolation of the estimated manifold between fitted data points. The proposed approach is motivated by novel theoretical properties of local covariance matrices constructed from noisy samples on a manifold. Our results enable us to turn a global manifold reconstruction problem into a local regression problem, allowing application of Gaussian processes for probabilistic manifold reconstruction. In addition to theory justifying the algorithm, we provide simulated and real data examples to illustrate the performance.

Diffusion Based Gaussian Processes on Restricted Domains

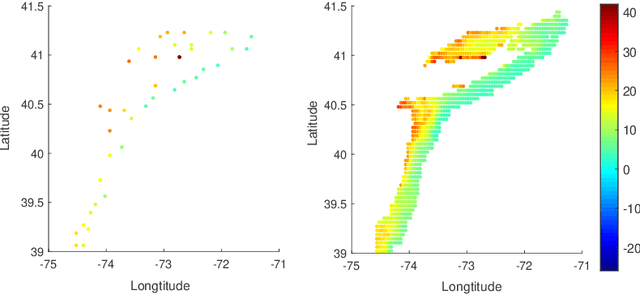
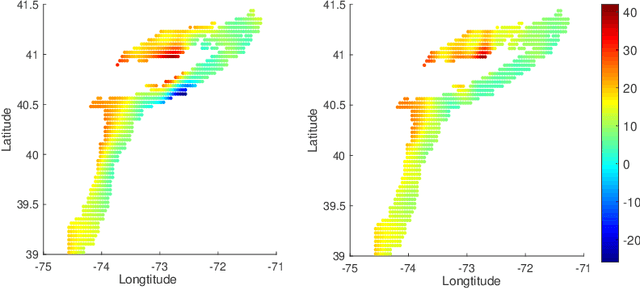
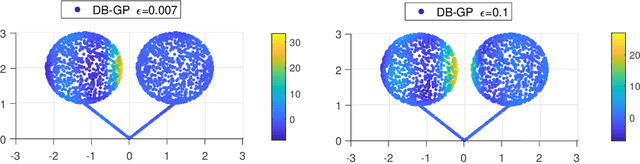
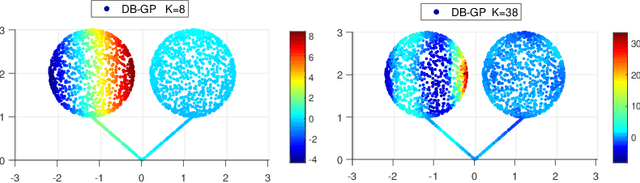
In nonparametric regression and spatial process modeling, it is common for the inputs to fall in a restricted subset of Euclidean space. For example, the locations at which spatial data are collected may be restricted to a narrow non-linear subset, such as near the edge of a lake. Typical kernel-based methods that do not take into account the intrinsic geometric of the domain across which observations are collected may produce sub-optimal results. In this article, we focus on solving this problem in the context of Gaussian process (GP) models, proposing a new class of diffusion-based GPs (DB-GPs), which learn a covariance that respects the geometry of the input domain. We use the term `diffusion-based' as the idea is to measure intrinsic distances between inputs in a restricted domain via a diffusion process. As the heat kernel is intractable computationally, we approximate the covariance using finitely-many eigenpairs of the Graph Laplacian (GL). Our proposed algorithm has the same order of computational complexity as current GP algorithms using simple covariance kernels. We provide substantial theoretical support for the DB-GP methodology, and illustrate performance gains through toy examples, simulation studies, and applications to ecology data.

Geodesic Distance Estimation with Spherelets

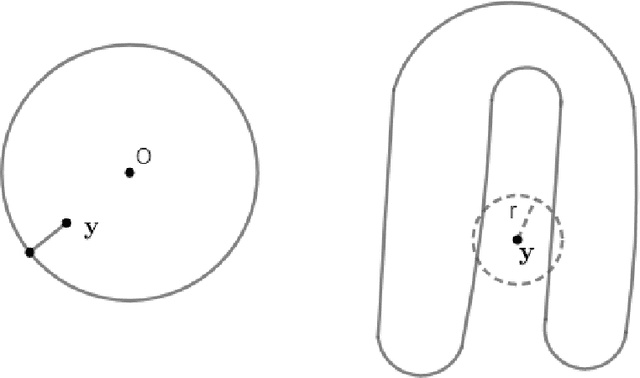
Many statistical and machine learning approaches rely on pairwise distances between data points. The choice of distance metric has a fundamental impact on performance of these procedures, raising questions about how to appropriately calculate distances. When data points are real-valued vectors, by far the most common choice is the Euclidean distance. This article is focused on the problem of how to better calculate distances taking into account the intrinsic geometry of the data, assuming data are concentrated near an unknown subspace or manifold. The appropriate geometric distance corresponds to the length of the shortest path along the manifold, which is the geodesic distance. When the manifold is unknown, it is challenging to accurately approximate the geodesic distance. Current algorithms are either highly complex, and hence often impractical to implement, or based on simple local linear approximations and shortest path algorithms that may have inadequate accuracy. We propose a simple and general alternative, which uses pieces of spheres, or spherelets, to locally approximate the unknown subspace and thereby estimate the geodesic distance through paths over spheres. Theory is developed showing lower error for many manifolds. This conclusion is supported through multiple simulation examples and applications to real data sets.

Classification via local manifold approximation

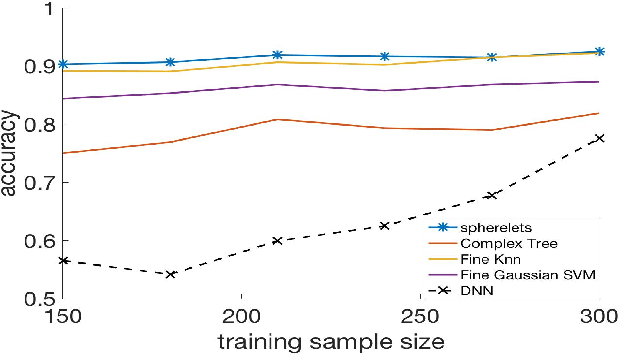
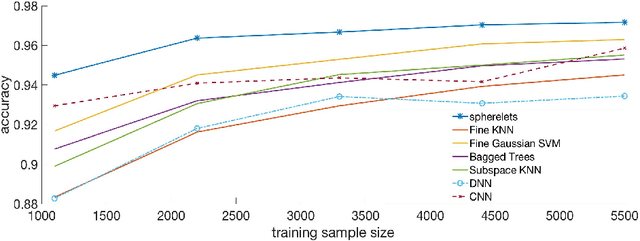
Classifiers label data as belonging to one of a set of groups based on input features. It is challenging to obtain accurate classification performance when the feature distributions in the different classes are complex, with nonlinear, overlapping and intersecting supports. This is particularly true when training data are limited. To address this problem, this article proposes a new type of classifier based on obtaining a local approximation to the support of the data within each class in a neighborhood of the feature to be classified, and assigning the feature to the class having the closest support. This general algorithm is referred to as LOcal Manifold Approximation (LOMA) classification. As a simple and theoretically supported special case having excellent performance in a broad variety of examples, we use spheres for local approximation, obtaining a SPherical Approximation (SPA) classifier. We illustrate substantial gains for SPA over competitors on a variety of challenging simulated and real data examples.

Clustering-Enhanced Stochastic Gradient MCMC for Hidden Markov Models with Rare States

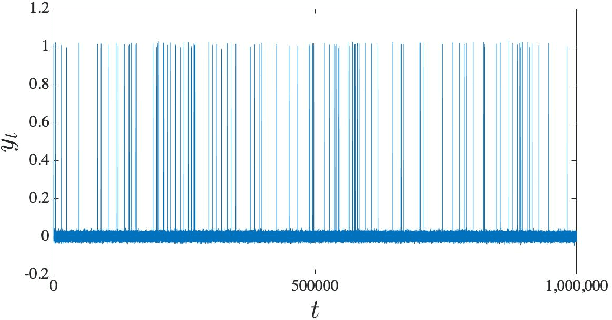
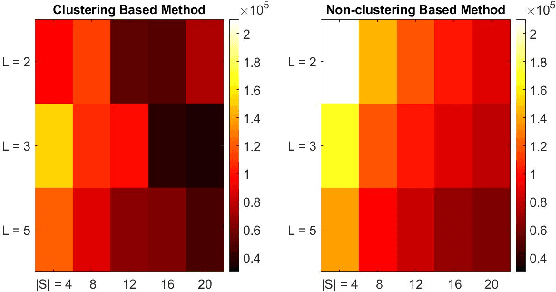
MCMC algorithms for hidden Markov models, which often rely on the forward-backward sampler, suffer with large sample size due to the temporal dependence inherent in the data. Recently, a number of approaches have been developed for posterior inference which make use of the mixing of the hidden Markov process to approximate the full posterior by using small chunks of the data. However, in the presence of imbalanced data resulting from rare latent states, the proposed minibatch estimates will often exclude rare state data resulting in poor inference of the associated emission parameters and inaccurate prediction or detection of rare events. Here, we propose to use a preliminary clustering to over-sample the rare clusters and reduce variance in gradient estimation within Stochastic Gradient MCMC. We demonstrate very substantial gains in predictive and inferential accuracy on real and synthetic examples.

Bayesian Distance Clustering

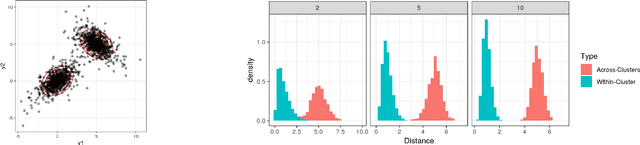
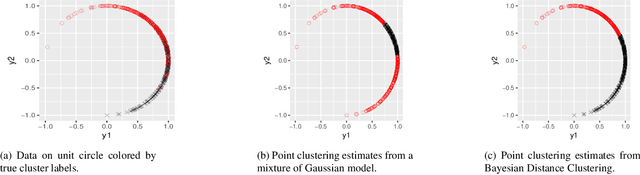
Model-based clustering is widely-used in a variety of application areas. However, fundamental concerns remain about robustness. In particular, results can be sensitive to the choice of kernel representing the within-cluster data density. Leveraging on properties of pairwise differences between data points, we propose a class of Bayesian distance clustering methods, which rely on modeling the likelihood of the pairwise distances in place of the original data. Although some information in the data is discarded, we gain substantial robustness to modeling assumptions. The proposed approach represents an appealing middle ground between distance- and model-based clustering, drawing advantages from each of these canonical approaches. We illustrate dramatic gains in the ability to infer clusters that are not well represented by the usual choices of kernel. A simulation study is included to assess performance relative to competitors, and we apply the approach to clustering of brain genome expression data. Keywords: Distance-based clustering; Mixture model; Model-based clustering; Model misspecification; Pairwise distance matrix; Partial likelihood; Robustness.