Diffusion Based Gaussian Processes on Restricted Domains

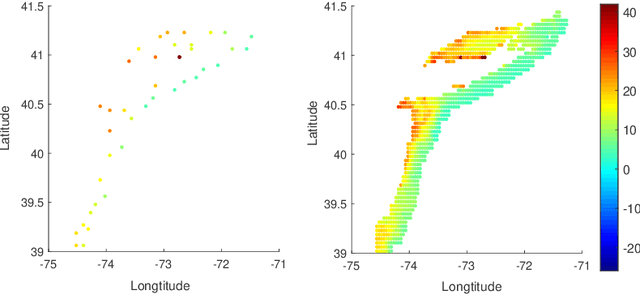
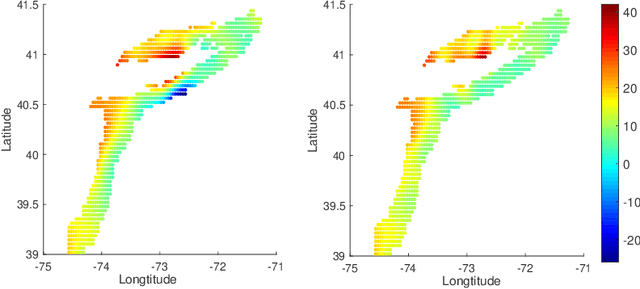
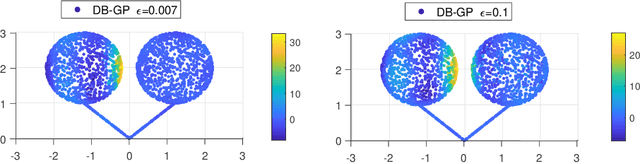
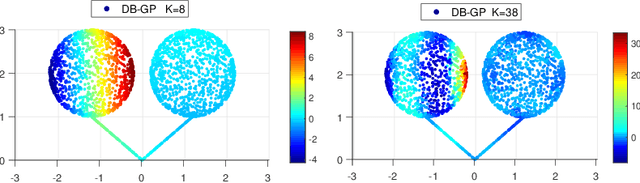
In nonparametric regression and spatial process modeling, it is common for the inputs to fall in a restricted subset of Euclidean space. For example, the locations at which spatial data are collected may be restricted to a narrow non-linear subset, such as near the edge of a lake. Typical kernel-based methods that do not take into account the intrinsic geometric of the domain across which observations are collected may produce sub-optimal results. In this article, we focus on solving this problem in the context of Gaussian process (GP) models, proposing a new class of diffusion-based GPs (DB-GPs), which learn a covariance that respects the geometry of the input domain. We use the term `diffusion-based' as the idea is to measure intrinsic distances between inputs in a restricted domain via a diffusion process. As the heat kernel is intractable computationally, we approximate the covariance using finitely-many eigenpairs of the Graph Laplacian (GL). Our proposed algorithm has the same order of computational complexity as current GP algorithms using simple covariance kernels. We provide substantial theoretical support for the DB-GP methodology, and illustrate performance gains through toy examples, simulation studies, and applications to ecology data.