Latent Simplex Position Model: High Dimensional Multi-view Clustering with Uncertainty Quantification

High dimensional data often contain multiple facets, and several clustering patterns (views) can co-exist under different feature subspaces. While multi-view clustering algorithms were proposed, the uncertainty quantification remains difficult --- a particular challenge is in the high complexity of estimating the cluster assignment probability under each view, or/and to efficiently share information across views. In this article, we propose an empirical Bayes approach --- viewing the similarity matrices generated over subspaces as rough first-stage estimates for co-assignment probabilities, in its Kullback-Leibler neighborhood we obtain a refined low-rank soft cluster graph, formed by the pairwise product of simplex coordinates. Interestingly, each simplex coordinate directly encodes the cluster assignment uncertainty. For multi-view clustering, we equip each similarity matrix with a mixed membership over a small number of latent views, leading to effective dimension reduction. With a high model flexibility, the estimation can be succinctly re-parameterized as a continuous optimization problem, hence enjoys gradient-based computation. Theory establishes the connection of this model to random cluster graph under multiple views. Compared to single-view clustering approaches, substantially more interpretable results are obtained when clustering brains from human traumatic brain injury study, using high-dimensional gene expression data. KEY WORDS: Co-regularized Clustering, Consensus, PAC-Bayes, Random Cluster Graph, Variable Selection

Bayesian Distance Clustering

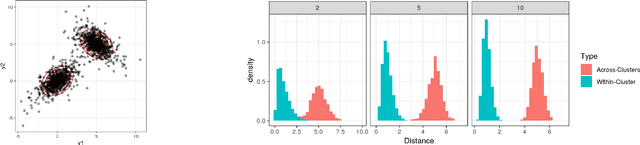
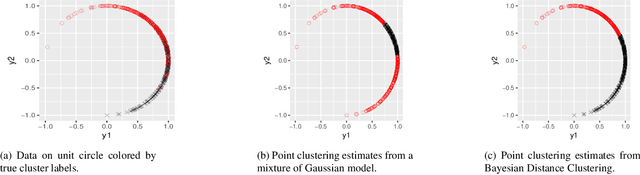
Model-based clustering is widely-used in a variety of application areas. However, fundamental concerns remain about robustness. In particular, results can be sensitive to the choice of kernel representing the within-cluster data density. Leveraging on properties of pairwise differences between data points, we propose a class of Bayesian distance clustering methods, which rely on modeling the likelihood of the pairwise distances in place of the original data. Although some information in the data is discarded, we gain substantial robustness to modeling assumptions. The proposed approach represents an appealing middle ground between distance- and model-based clustering, drawing advantages from each of these canonical approaches. We illustrate dramatic gains in the ability to infer clusters that are not well represented by the usual choices of kernel. A simulation study is included to assess performance relative to competitors, and we apply the approach to clustering of brain genome expression data. Keywords: Distance-based clustering; Mixture model; Model-based clustering; Model misspecification; Pairwise distance matrix; Partial likelihood; Robustness.