Neural Block Sampling

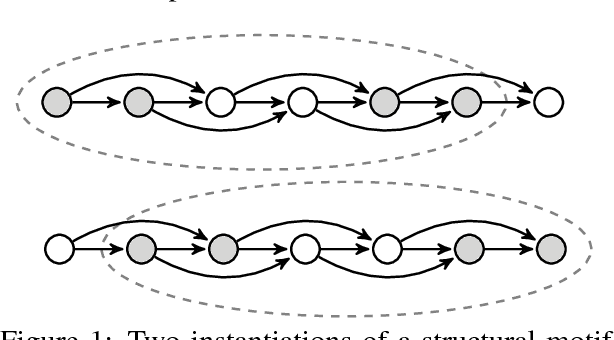
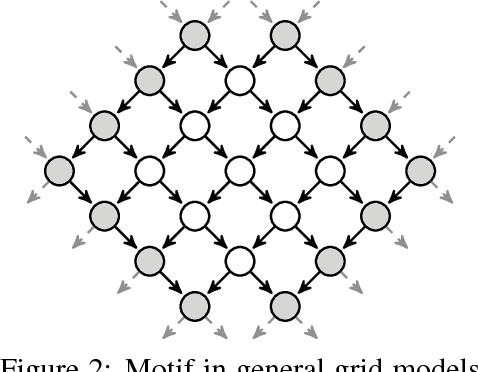
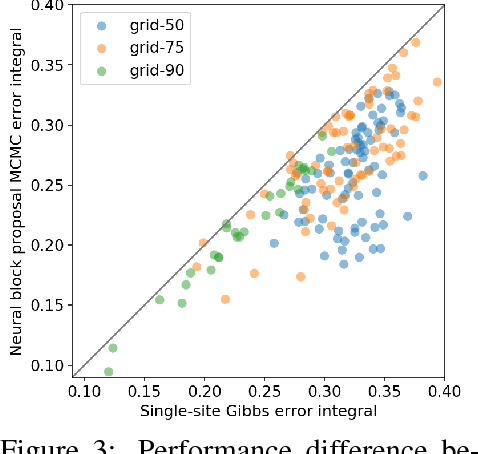
Efficient Monte Carlo inference often requires manual construction of model-specific proposals. We propose an approach to automated proposal construction by training neural networks to provide fast approximations to block Gibbs conditionals. The learned proposals generalize to occurrences of common structural motifs both within a given model and across models, allowing for the construction of a library of learned inference primitives that can accelerate inference on unseen models with no model-specific training required. We explore several applications including open-universe Gaussian mixture models, in which our learned proposals outperform a hand-tuned sampler, and a real-world named entity recognition task, in which our sampler's ability to escape local modes yields higher final F1 scores than single-site Gibbs.

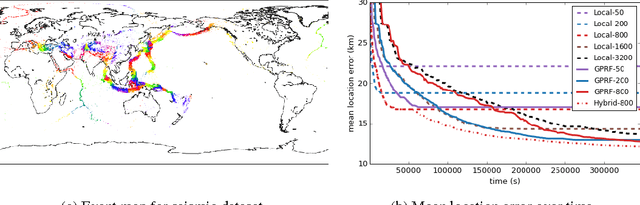
Signal-based Bayesian Seismic Monitoring

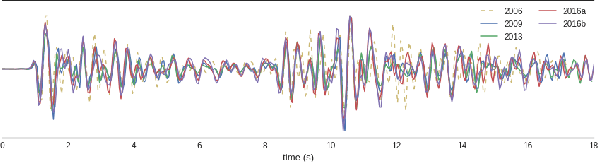
Detecting weak seismic events from noisy sensors is a difficult perceptual task. We formulate this task as Bayesian inference and propose a generative model of seismic events and signals across a network of spatially distributed stations. Our system, SIGVISA, is the first to directly model seismic waveforms, allowing it to incorporate a rich representation of the physics underlying the signal generation process. We use Gaussian processes over wavelet parameters to predict detailed waveform fluctuations based on historical events, while degrading smoothly to simple parametric envelopes in regions with no historical seismicity. Evaluating on data from the western US, we recover three times as many events as previous work, and reduce mean location errors by a factor of four while greatly increasing sensitivity to low-magnitude events.

Parallel Chromatic MCMC with Spatial Partitioning

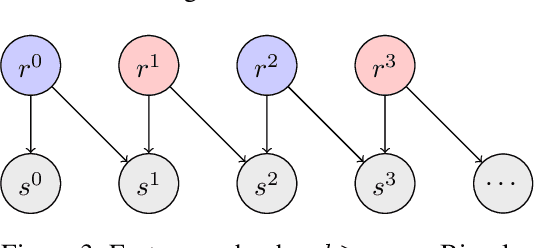
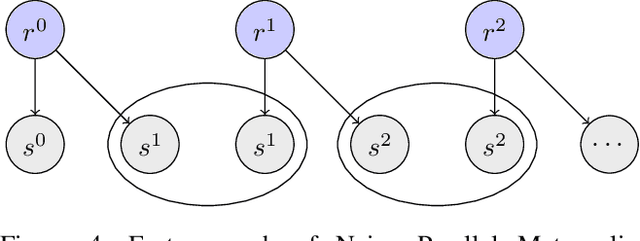
We introduce a novel approach for parallelizing MCMC inference in models with spatially determined conditional independence relationships, for which existing techniques exploiting graphical model structure are not applicable. Our approach is motivated by a model of seismic events and signals, where events detected in distant regions are approximately independent given those in intermediate regions. We perform parallel inference by coloring a factor graph defined over regions of latent space, rather than individual model variables. Evaluating on a model of seismic event detection, we achieve significant speedups over serial MCMC with no degradation in inference quality.

Gaussian Process Random Fields

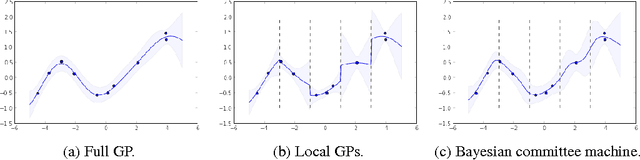
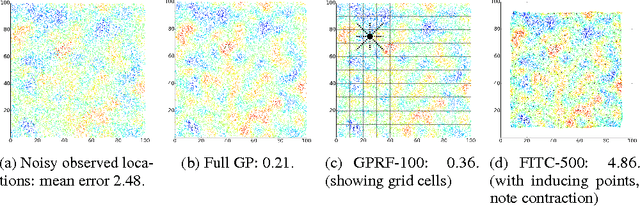
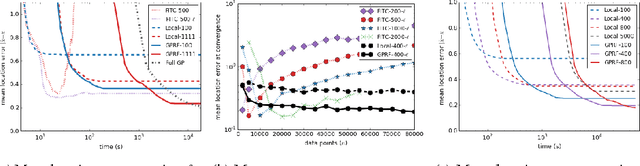
Gaussian processes have been successful in both supervised and unsupervised machine learning tasks, but their computational complexity has constrained practical applications. We introduce a new approximation for large-scale Gaussian processes, the Gaussian Process Random Field (GPRF), in which local GPs are coupled via pairwise potentials. The GPRF likelihood is a simple, tractable, and parallelizeable approximation to the full GP marginal likelihood, enabling latent variable modeling and hyperparameter selection on large datasets. We demonstrate its effectiveness on synthetic spatial data as well as a real-world application to seismic event location.