Gaussian Process Random Fields
Paper and Code
Oct 31, 2015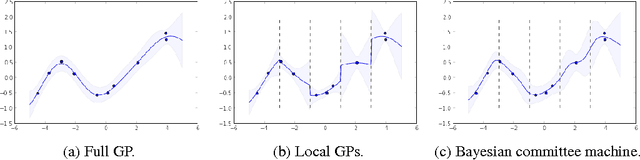
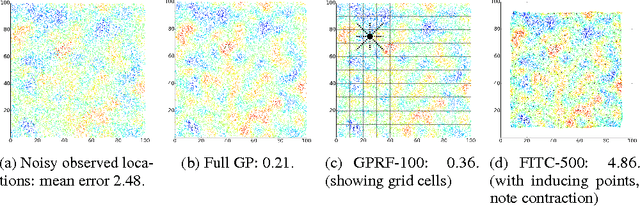
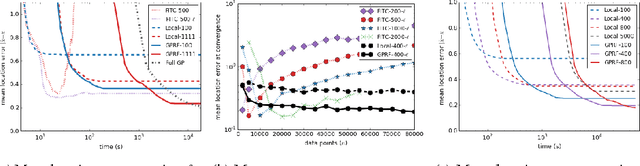
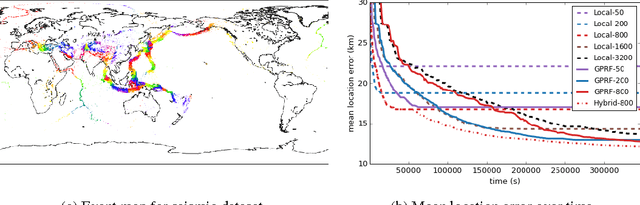
Gaussian processes have been successful in both supervised and unsupervised machine learning tasks, but their computational complexity has constrained practical applications. We introduce a new approximation for large-scale Gaussian processes, the Gaussian Process Random Field (GPRF), in which local GPs are coupled via pairwise potentials. The GPRF likelihood is a simple, tractable, and parallelizeable approximation to the full GP marginal likelihood, enabling latent variable modeling and hyperparameter selection on large datasets. We demonstrate its effectiveness on synthetic spatial data as well as a real-world application to seismic event location.
* Advances in Neural Information Processing Systems (NIPS), 2015
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge