Daniel Schneegass
RelSen: An Optimization-based Framework for Simultaneous Sensor Reliability Monitoring and Process State Estimation
Apr 19, 2020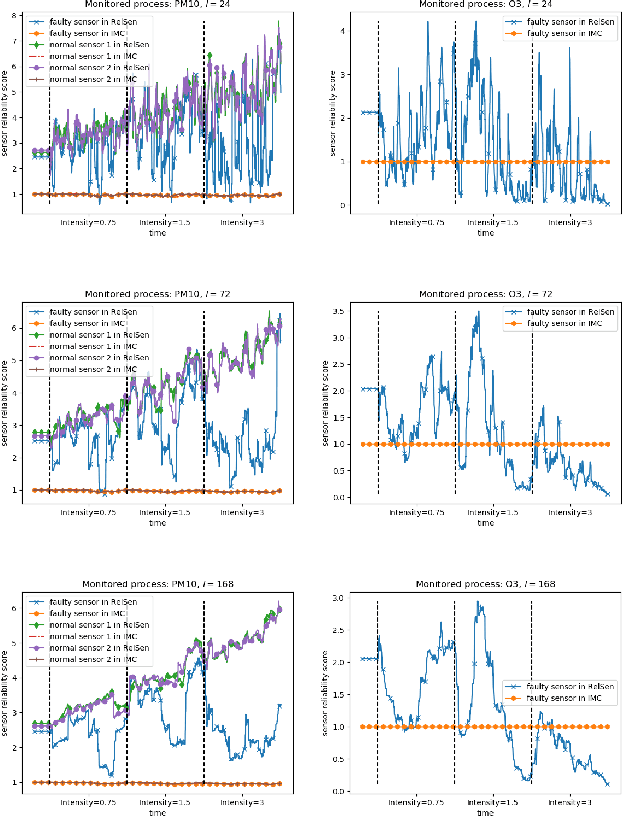



Abstract:Recent advances in the Internet of Things (IoT) technology have led to a surge on the deployment of sensors everywhere. As a result, information obtained from sensors has become an important source for decision making in our daily life. Unfortunately, in most sensing applications, sensors are known to be error-prone due to various reasons and the measurements from sensors can also become unreliable at any unexpected time. Therefore, apart from the states of physical processes under measurement, we believe it is highly important to monitor the reliability of sensors as well. In this work, we propose RelSen: an optimization-based framework for simultaneous sensor reliability monitoring and process state estimation. In RelSen we formulate both the reliability scores of sensors and the states of monitored processes as variables to learn via an optimization problem only given the observed measurements from sensors. The optimization problem is efficiently solved by utilizing the redundancy of sensors, the correlation between multiple process states and the smoothness of each individual process. Furthermore, we apply RelSen for sensor reliability monitoring and process state estimation in an outdoor air pollution monitoring system and the condition monitoring system for a cement rotary kiln. Experimental results show that our framework can timely identify unreliable sensors and achieve higher accuracy than several baseline methods in process state estimation under three types of commonly observed sensor faults.
A Search for the Underlying Equation Governing Similar Systems
Aug 27, 2019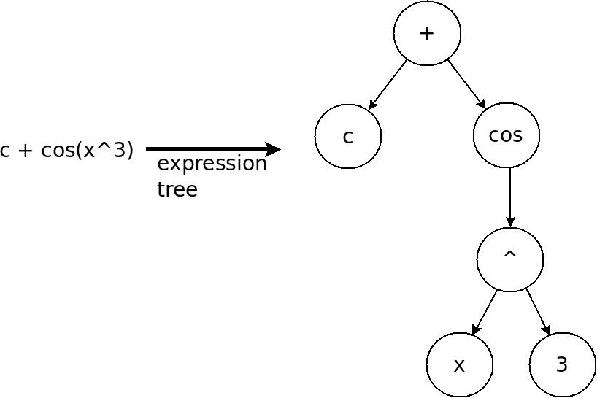
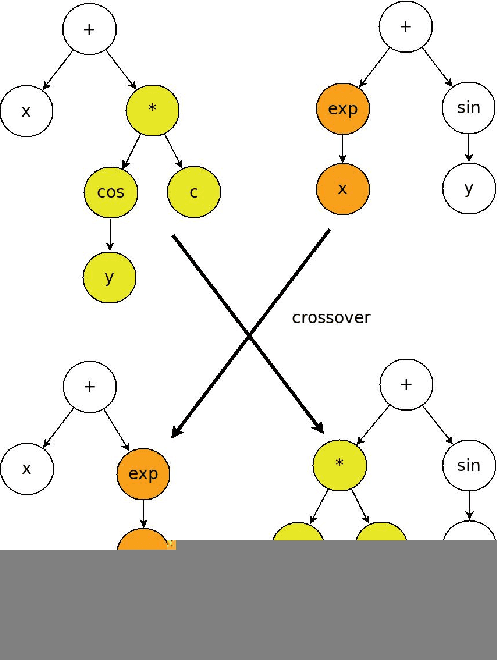
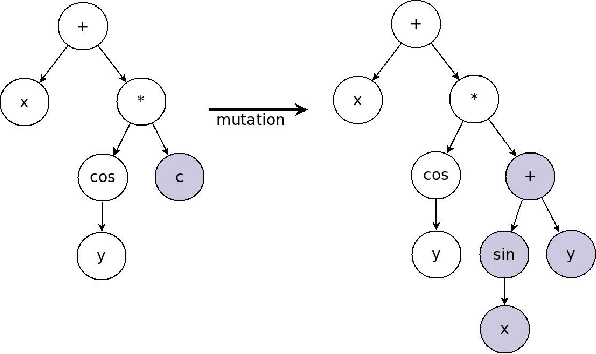
Abstract:We show a data-driven approach to discover the underlying structural form of the mathematical equation governing the dynamics of multiple but similar systems induced by the same mechanisms. This approach hinges on theories that we lay out involving arguments based on the nature of physical systems. In the same vein, we also introduce a metric to search for the best candidate equation using the datasets generated from the systems. This approach involves symbolic regression by means of genetic programming and regressions to compute the strength of the interplay between the extrinsic parameters in a candidate equation. We relate these extrinsic parameters to the hidden properties of the data-generating systems. The behavior of a new similar system can be predicted easily by utilizing the discovered structural form of the general equation. As illustrations, we apply the approach to identify candidate structural forms of the underlying equation governing two cases: the changes in a sensor measurement of degrading engines; and the search for the governing equation of systems with known variations of an intrinsic parameter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge