A Search for the Underlying Equation Governing Similar Systems
Paper and Code
Aug 27, 2019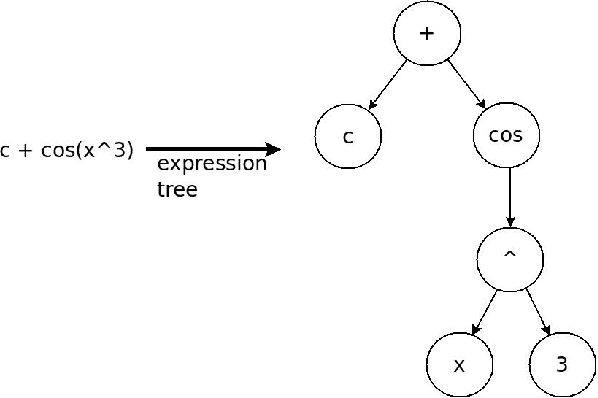
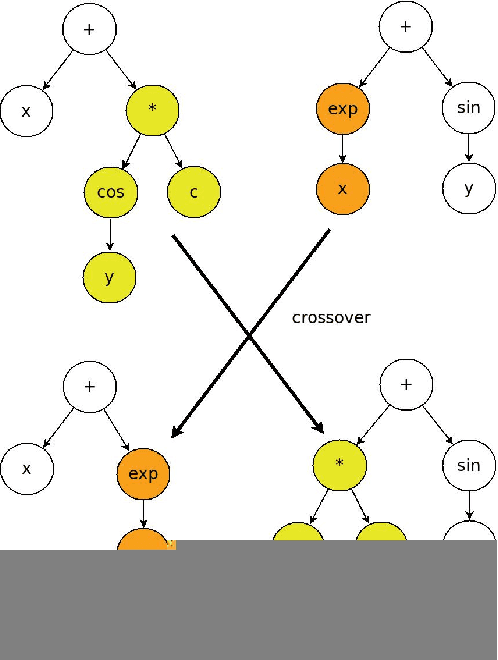
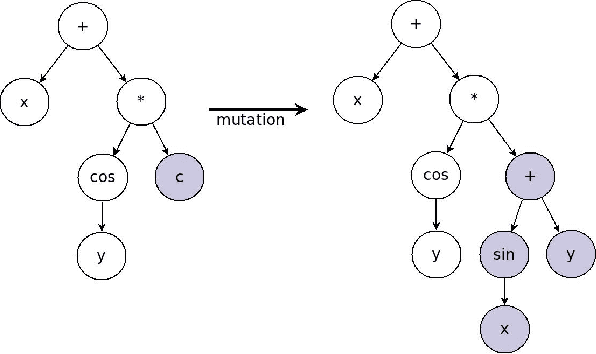
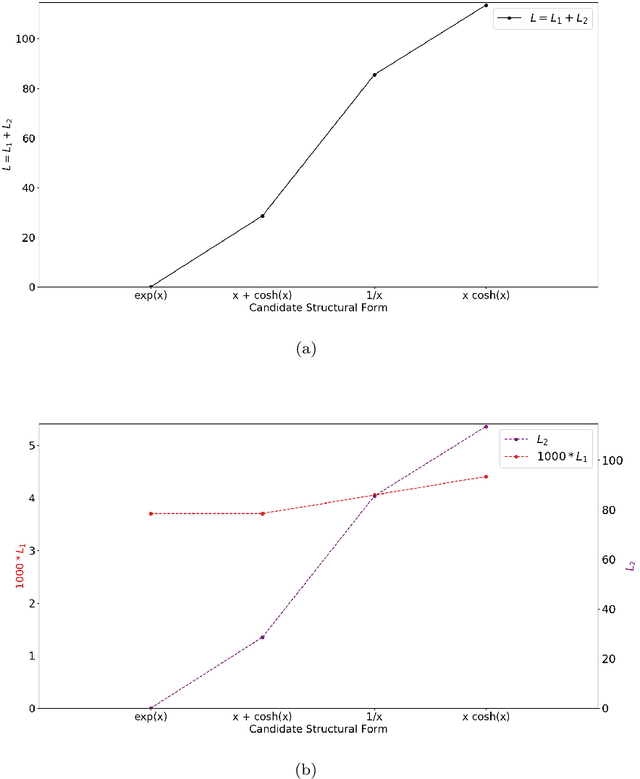
We show a data-driven approach to discover the underlying structural form of the mathematical equation governing the dynamics of multiple but similar systems induced by the same mechanisms. This approach hinges on theories that we lay out involving arguments based on the nature of physical systems. In the same vein, we also introduce a metric to search for the best candidate equation using the datasets generated from the systems. This approach involves symbolic regression by means of genetic programming and regressions to compute the strength of the interplay between the extrinsic parameters in a candidate equation. We relate these extrinsic parameters to the hidden properties of the data-generating systems. The behavior of a new similar system can be predicted easily by utilizing the discovered structural form of the general equation. As illustrations, we apply the approach to identify candidate structural forms of the underlying equation governing two cases: the changes in a sensor measurement of degrading engines; and the search for the governing equation of systems with known variations of an intrinsic parameter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge