Time Series Anomaly Detection for Cyber-physical Systems via Neural System Identification and Bayesian Filtering

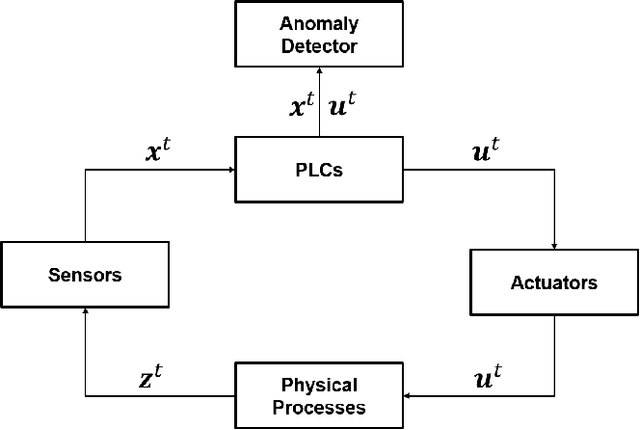
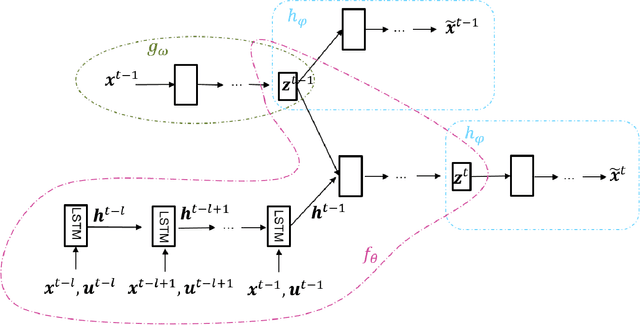
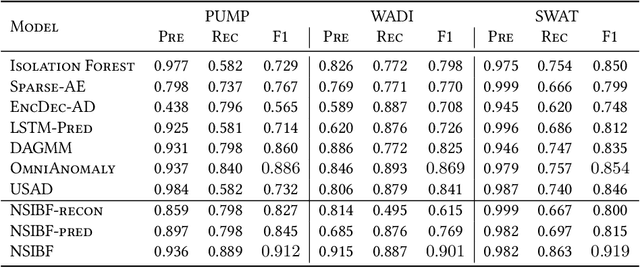
Recent advances in AIoT technologies have led to an increasing popularity of utilizing machine learning algorithms to detect operational failures for cyber-physical systems (CPS). In its basic form, an anomaly detection module monitors the sensor measurements and actuator states from the physical plant, and detects anomalies in these measurements to identify abnormal operation status. Nevertheless, building effective anomaly detection models for CPS is rather challenging as the model has to accurately detect anomalies in presence of highly complicated system dynamics and unknown amount of sensor noise. In this work, we propose a novel time series anomaly detection method called Neural System Identification and Bayesian Filtering (NSIBF) in which a specially crafted neural network architecture is posed for system identification, i.e., capturing the dynamics of CPS in a dynamical state-space model; then a Bayesian filtering algorithm is naturally applied on top of the "identified" state-space model for robust anomaly detection by tracking the uncertainty of the hidden state of the system recursively over time. We provide qualitative as well as quantitative experiments with the proposed method on a synthetic and three real-world CPS datasets, showing that NSIBF compares favorably to the state-of-the-art methods with considerable improvements on anomaly detection in CPS.

A Search for the Underlying Equation Governing Similar Systems

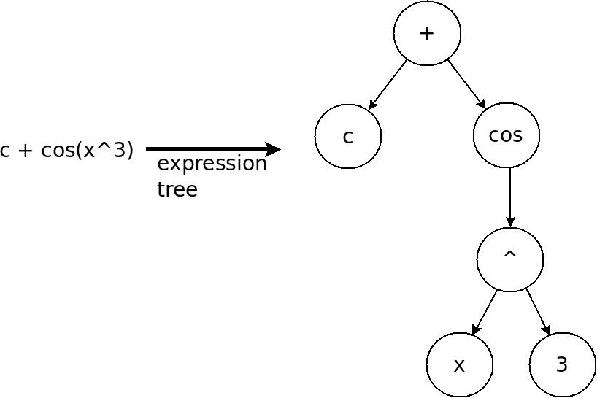
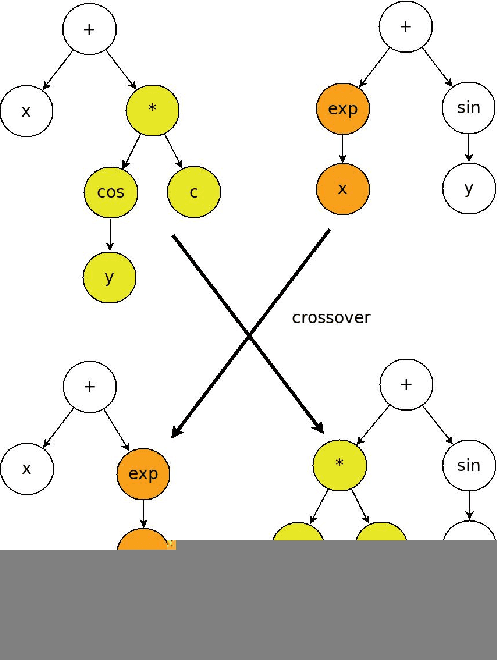
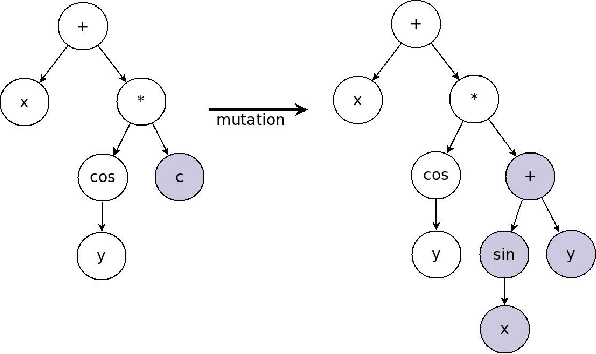
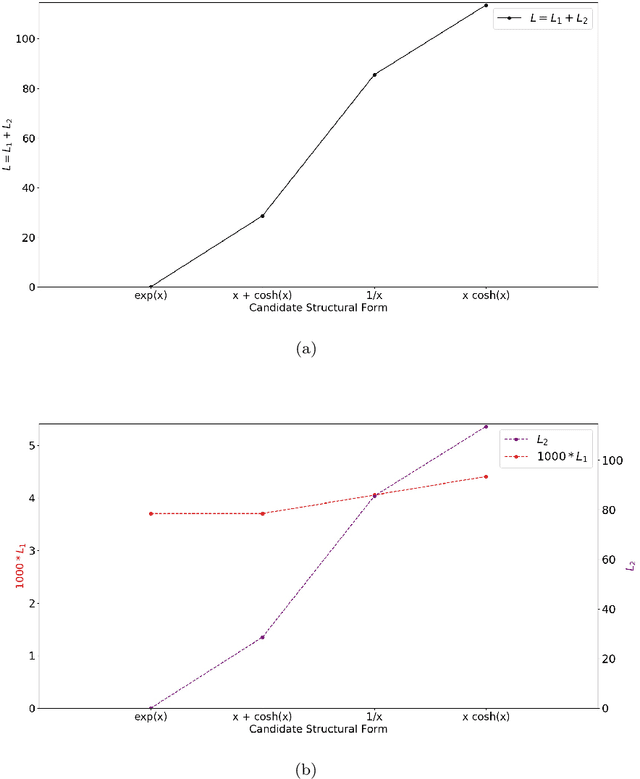
We show a data-driven approach to discover the underlying structural form of the mathematical equation governing the dynamics of multiple but similar systems induced by the same mechanisms. This approach hinges on theories that we lay out involving arguments based on the nature of physical systems. In the same vein, we also introduce a metric to search for the best candidate equation using the datasets generated from the systems. This approach involves symbolic regression by means of genetic programming and regressions to compute the strength of the interplay between the extrinsic parameters in a candidate equation. We relate these extrinsic parameters to the hidden properties of the data-generating systems. The behavior of a new similar system can be predicted easily by utilizing the discovered structural form of the general equation. As illustrations, we apply the approach to identify candidate structural forms of the underlying equation governing two cases: the changes in a sensor measurement of degrading engines; and the search for the governing equation of systems with known variations of an intrinsic parameter.