A Perturbation Bound on the Subspace Estimator from Canonical Projections

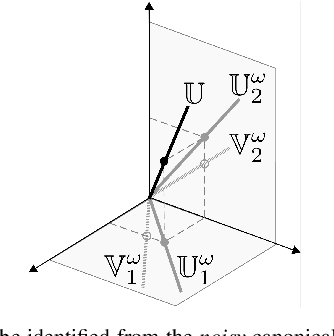
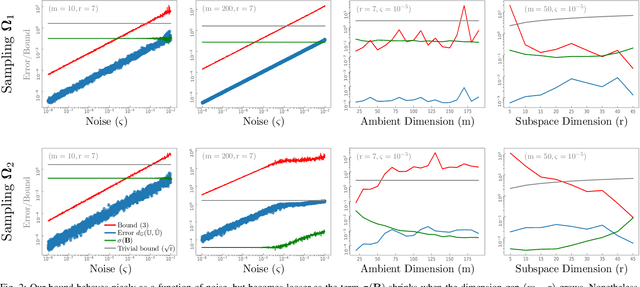
This paper derives a perturbation bound on the optimal subspace estimator obtained from a subset of its canonical projections contaminated by noise. This fundamental result has important implications in matrix completion, subspace clustering, and related problems.

Fusion Subspace Clustering: Full and Incomplete Data

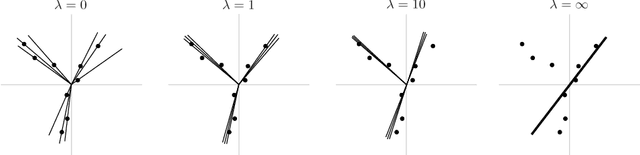
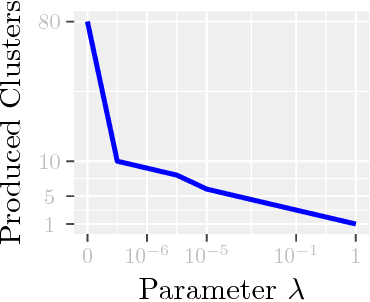
Modern inference and learning often hinge on identifying low-dimensional structures that approximate large scale data. Subspace clustering achieves this through a union of linear subspaces. However, in contemporary applications data is increasingly often incomplete, rendering standard (full-data) methods inapplicable. On the other hand, existing incomplete-data methods present major drawbacks, like lifting an already high-dimensional problem, or requiring a super polynomial number of samples. Motivated by this, we introduce a new subspace clustering algorithm inspired by fusion penalties. The main idea is to permanently assign each datum to a subspace of its own, and minimize the distance between the subspaces of all data, so that subspaces of the same cluster get fused together. Our approach is entirely new to both, full and missing data, and unlike other methods, it directly allows noise, it requires no liftings, it allows low, high, and even full-rank data, it approaches optimal (information-theoretic) sampling rates, and it does not rely on other methods such as low-rank matrix completion to handle missing data. Furthermore, our extensive experiments on both real and synthetic data show that our approach performs comparably to the state-of-the-art with complete data, and dramatically better if data is missing.

Mixture Matrix Completion

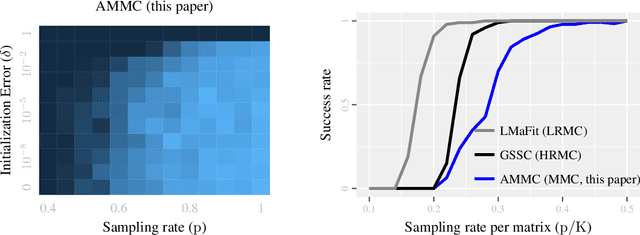
Completing a data matrix X has become an ubiquitous problem in modern data science, with applications in recommender systems, computer vision, and networks inference, to name a few. One typical assumption is that X is low-rank. A more general model assumes that each column of X corresponds to one of several low-rank matrices. This paper generalizes these models to what we call mixture matrix completion (MMC): the case where each entry of X corresponds to one of several low-rank matrices. MMC is a more accurate model for recommender systems, and brings more flexibility to other completion and clustering problems. We make four fundamental contributions about this new model. First, we show that MMC is theoretically possible (well-posed). Second, we give its precise information-theoretic identifiability conditions. Third, we derive the sample complexity of MMC. Finally, we give a practical algorithm for MMC with performance comparable to the state-of-the-art for simpler related problems, both on synthetic and real data.

A Characterization of Deterministic Sampling Patterns for Low-Rank Matrix Completion

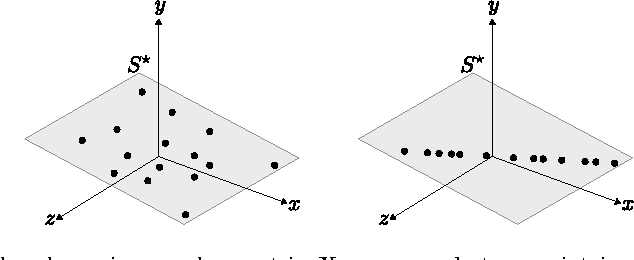
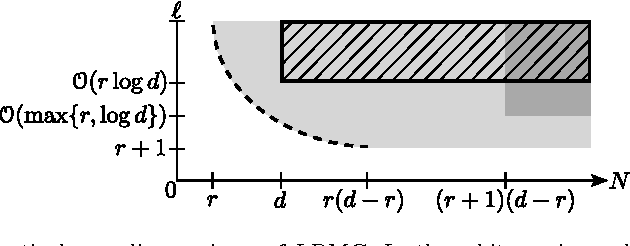
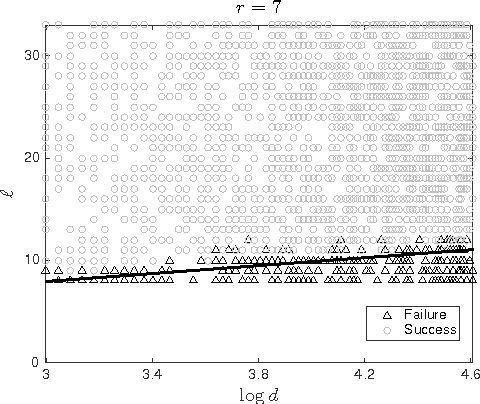
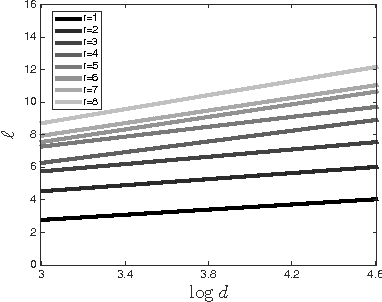
Low-rank matrix completion (LRMC) problems arise in a wide variety of applications. Previous theory mainly provides conditions for completion under missing-at-random samplings. This paper studies deterministic conditions for completion. An incomplete $d \times N$ matrix is finitely rank-$r$ completable if there are at most finitely many rank-$r$ matrices that agree with all its observed entries. Finite completability is the tipping point in LRMC, as a few additional samples of a finitely completable matrix guarantee its unique completability. The main contribution of this paper is a deterministic sampling condition for finite completability. We use this to also derive deterministic sampling conditions for unique completability that can be efficiently verified. We also show that under uniform random sampling schemes, these conditions are satisfied with high probability if $O(\max\{r,\log d\})$ entries per column are observed. These findings have several implications on LRMC regarding lower bounds, sample and computational complexity, the role of coherence, adaptive settings and the validation of any completion algorithm. We complement our theoretical results with experiments that support our findings and motivate future analysis of uncharted sampling regimes.

Deterministic Conditions for Subspace Identifiability from Incomplete Sampling

Consider a generic $r$-dimensional subspace of $\mathbb{R}^d$, $r<d$, and suppose that we are only given projections of this subspace onto small subsets of the canonical coordinates. The paper establishes necessary and sufficient deterministic conditions on the subsets for subspace identifiability.

To lie or not to lie in a subspace

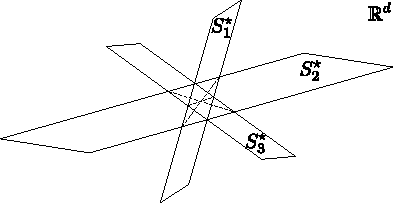
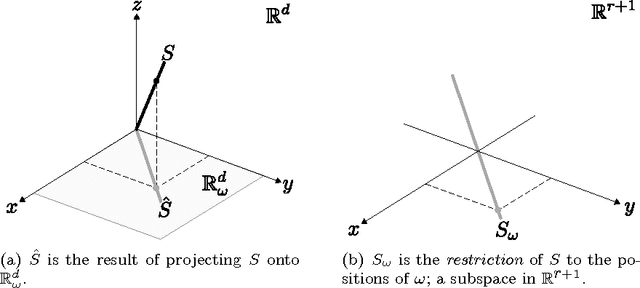
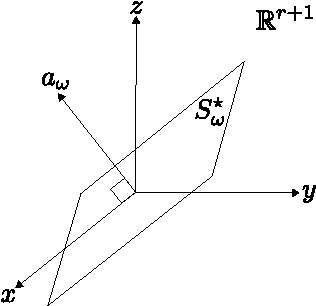
Give deterministic necessary and sufficient conditions to guarantee that if a subspace fits certain partially observed data from a union of subspaces, it is because such data really lies in a subspace. Furthermore, Give deterministic necessary and sufficient conditions to guarantee that if a subspace fits certain partially observed data, such subspace is unique. Do this by characterizing when and only when a set of incomplete vectors behaves as a single but complete one.