A Characterization of Deterministic Sampling Patterns for Low-Rank Matrix Completion

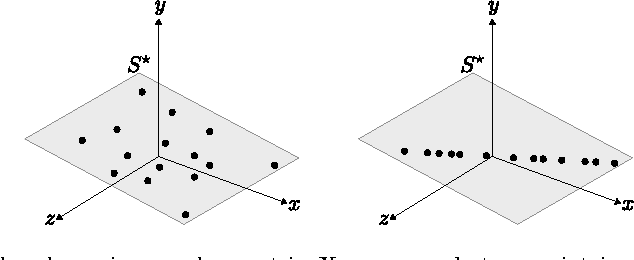
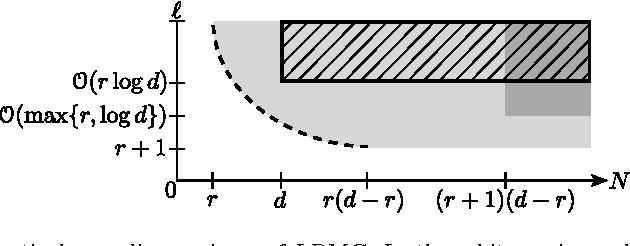
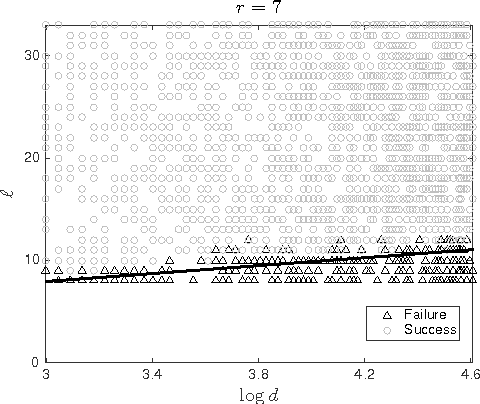
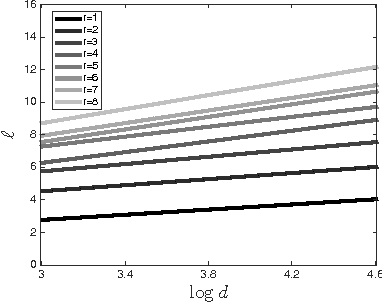
Low-rank matrix completion (LRMC) problems arise in a wide variety of applications. Previous theory mainly provides conditions for completion under missing-at-random samplings. This paper studies deterministic conditions for completion. An incomplete $d \times N$ matrix is finitely rank-$r$ completable if there are at most finitely many rank-$r$ matrices that agree with all its observed entries. Finite completability is the tipping point in LRMC, as a few additional samples of a finitely completable matrix guarantee its unique completability. The main contribution of this paper is a deterministic sampling condition for finite completability. We use this to also derive deterministic sampling conditions for unique completability that can be efficiently verified. We also show that under uniform random sampling schemes, these conditions are satisfied with high probability if $O(\max\{r,\log d\})$ entries per column are observed. These findings have several implications on LRMC regarding lower bounds, sample and computational complexity, the role of coherence, adaptive settings and the validation of any completion algorithm. We complement our theoretical results with experiments that support our findings and motivate future analysis of uncharted sampling regimes.

Deterministic Conditions for Subspace Identifiability from Incomplete Sampling

Consider a generic $r$-dimensional subspace of $\mathbb{R}^d$, $r<d$, and suppose that we are only given projections of this subspace onto small subsets of the canonical coordinates. The paper establishes necessary and sufficient deterministic conditions on the subsets for subspace identifiability.