A theory of learning with constrained weight-distribution

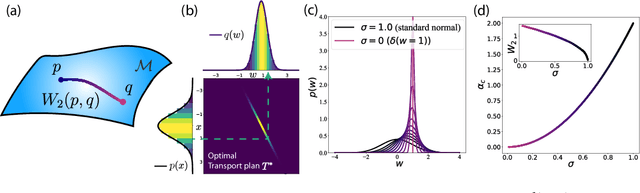
A central question in computational neuroscience is how structure determines function in neural networks. The emerging high-quality large-scale connectomic datasets raise the question of what general functional principles can be gleaned from structural information such as the distribution of excitatory/inhibitory synapse types and the distribution of synaptic weights. Motivated by this question, we developed a statistical mechanical theory of learning in neural networks that incorporates structural information as constraints. We derived an analytical solution for the memory capacity of the perceptron, a basic feedforward model of supervised learning, with constraint on the distribution of its weights. Our theory predicts that the reduction in capacity due to the constrained weight-distribution is related to the Wasserstein distance between the imposed distribution and that of the standard normal distribution. To test the theoretical predictions, we use optimal transport theory and information geometry to develop an SGD-based algorithm to find weights that simultaneously learn the input-output task and satisfy the distribution constraint. We show that training in our algorithm can be interpreted as geodesic flows in the Wasserstein space of probability distributions. We further developed a statistical mechanical theory for teacher-student perceptron rule learning and ask for the best way for the student to incorporate prior knowledge of the rule. Our theory shows that it is beneficial for the learner to adopt different prior weight distributions during learning, and shows that distribution-constrained learning outperforms unconstrained and sign-constrained learning. Our theory and algorithm provide novel strategies for incorporating prior knowledge about weights into learning, and reveal a powerful connection between structure and function in neural networks.

Higher-Order Function Networks for Learning Composable 3D Object Representations

We present a method to represent 3D objects using higher order functions, where an object is encoded directly into the weights and biases of a small `mapping' network by a larger encoder network. This mapping network can be used to reconstruct 3D objects by applying its encoded transformation to points sampled from a simple canonical space. We first demonstrate that an encoder network can produce mappings that reconstruct objects from single images more accurately than state of the art point set reconstruction methods. Next, we show that our method yields meaningful gains for robot motion planning problems that use this object representation for collision avoidance. We also demonstrate that our formulation allows for a novel method of object interpolation in a latent function space, where we compose the roots of the reconstruction functions for various objects to generate new, coherent objects. Finally, we demonstrate the coding efficiency of our approach: encoding objects directly as a neural network is highly parameter efficient when compared with object representations that encode the object of interest as a latent vector `codeword'. Our smallest reconstruction network has only about 7000 parameters and shows reconstruction quality generally better than state-of-the-art codeword-based object representation architectures with millions of parameters.