Instrumenting an SMT Solver to Solve Hybrid Network Reachability Problems

PDDL+ planning has its semantics rooted in hybrid automata (HA) and recent work has shown that it can be modeled as a network of HAs. Addressing the complexity of nonlinear PDDL+ planning as HAs requires both space and time efficient reasoning. Unfortunately, existing solvers either do not address nonlinear dynamics or do not natively support networks of automata. We present a new algorithm, called HNSolve, which guides the variable selection of the dReal Satisfiability Modulo Theories (SMT) solver while reasoning about network encodings of nonlinear PDDL+ planning as HAs. HNSolve tightly integrates with dReal by solving a discrete abstraction of the HA network. HNSolve finds composite runs on the HA network that ignore continuous variables, but respect mode jumps and synchronization labels. HNSolve admissibly detects dead-ends in the discrete abstraction, and posts conflict clauses that prune the SMT solver's search. We evaluate the benefits of our HNSolve algorithm on PDDL+ benchmark problems and demonstrate its performance with respect to prior work.

Cost Sensitive Reachability Heuristics for Handling State Uncertainty

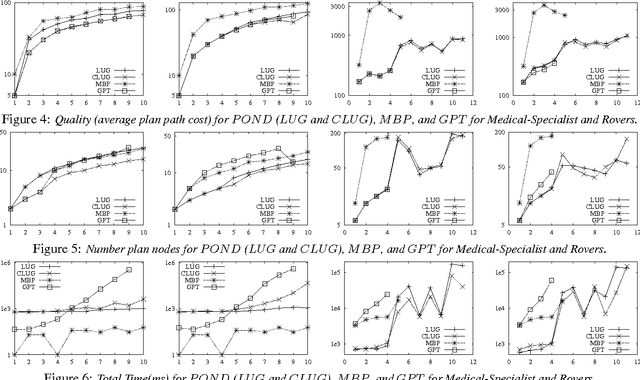
While POMDPs provide a general platform for non-deterministic conditional planning under a variety of quality metrics they have limited scalability. On the other hand, non-deterministic conditional planners scale very well, but many lack the ability to optimize plan quality metrics. We present a novel generalization of planning graph based heuristics that helps conditional planners both scale and generate high quality plans when using actions with nonuniform costs. We make empirical comparisons with two state of the art planners to show the benefit of our techniques.