Instrumenting an SMT Solver to Solve Hybrid Network Reachability Problems
Paper and Code
Sep 13, 2016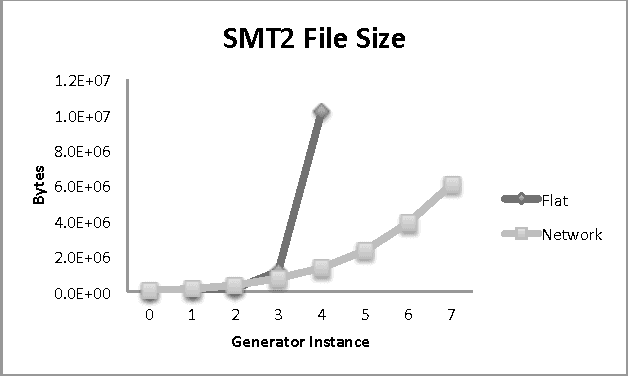
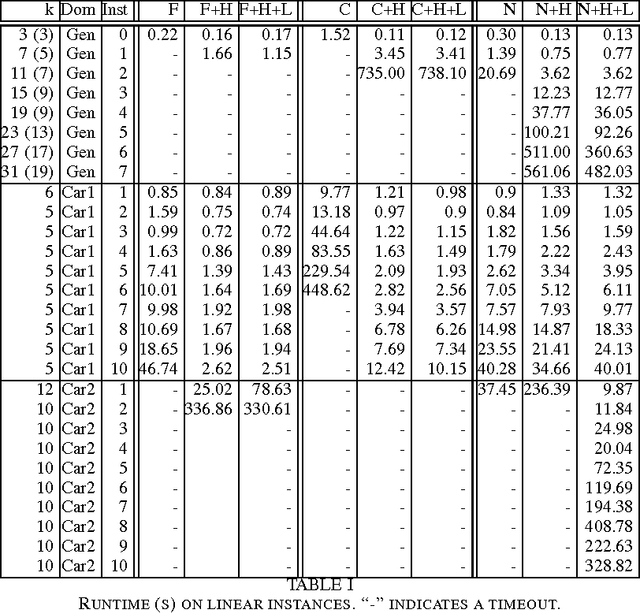

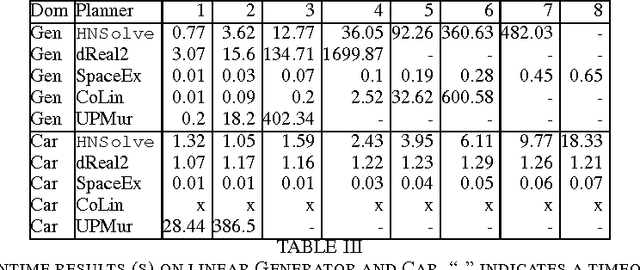
PDDL+ planning has its semantics rooted in hybrid automata (HA) and recent work has shown that it can be modeled as a network of HAs. Addressing the complexity of nonlinear PDDL+ planning as HAs requires both space and time efficient reasoning. Unfortunately, existing solvers either do not address nonlinear dynamics or do not natively support networks of automata. We present a new algorithm, called HNSolve, which guides the variable selection of the dReal Satisfiability Modulo Theories (SMT) solver while reasoning about network encodings of nonlinear PDDL+ planning as HAs. HNSolve tightly integrates with dReal by solving a discrete abstraction of the HA network. HNSolve finds composite runs on the HA network that ignore continuous variables, but respect mode jumps and synchronization labels. HNSolve admissibly detects dead-ends in the discrete abstraction, and posts conflict clauses that prune the SMT solver's search. We evaluate the benefits of our HNSolve algorithm on PDDL+ benchmark problems and demonstrate its performance with respect to prior work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge