Nonlinear Principal Component Analysis with Random Bernoulli Features for Process Monitoring

The process generates substantial amounts of data with highly complex structures, leading to the development of numerous nonlinear statistical methods. However, most of these methods rely on computations involving large-scale dense kernel matrices. This dependence poses significant challenges in meeting the high computational demands and real-time responsiveness required by online monitoring systems. To alleviate the computational burden of dense large-scale matrix multiplication, we incorporate the bootstrap sampling concept into random feature mapping and propose a novel random Bernoulli principal component analysis method to efficiently capture nonlinear patterns in the process. We derive a convergence bound for the kernel matrix approximation constructed using random Bernoulli features, ensuring theoretical robustness. Subsequently, we design four fast process monitoring methods based on random Bernoulli principal component analysis to extend its nonlinear capabilities for handling diverse fault scenarios. Finally, numerical experiments and real-world data analyses are conducted to evaluate the performance of the proposed methods. Results demonstrate that the proposed methods offer excellent scalability and reduced computational complexity, achieving substantial cost savings with minimal performance loss compared to traditional kernel-based approaches.

Fast Capacity Estimation in Ultra-dense Wireless Networks with Random Interference

In wireless communication systems, the accurate and reliable evaluation of channel capacity is believed to be a fundamental and critical issue for terminals. However, with the rapid development of wireless technology, large-scale communication networks with significant random interference have emerged, resulting in extremely high computational costs for capacity calculation. In ultra-dense wireless networks with extremely large numbers of base stations (BSs) and users, we provide fast estimation methods for determining the capacity. We consider two scenarios according to the ratio of the number of users to the number of BSs, $\beta_m$. First, when $\beta_m\leq1$, the FIsher-Spiked Estimation (FISE) algorithm is proposed to determine the capacity by modeling the channel matrix with random interference as a Fisher matrix. Second, when $\beta_m>1$, based on a closed-form expression for capacity estimation requiring solely simple computations, we prove that this estimation stabilizes and remains invariant with increasing $\beta_m$. Our methods can guarantee high accuracy on capacity estimation with low complexity, which is faster than the existing methods. Furthermore, our approaches exhibit excellent generality, free of network area shapes, BS and user distributions, and sub-network locations. Extensive simulation experiments across various scenarios demonstrate the high accuracy and robustness of our methods.

TOSE: A Fast Capacity Estimation Algorithm Based on Spike Approximations

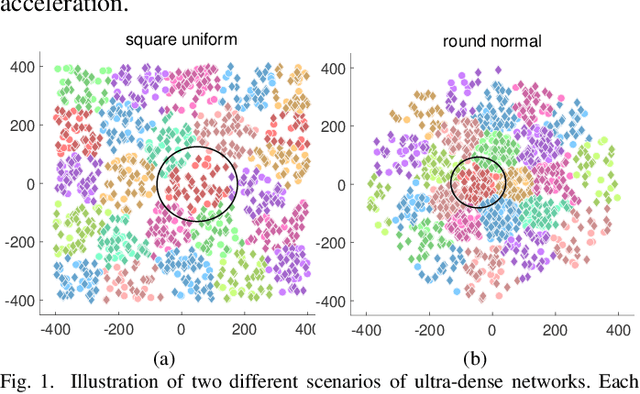
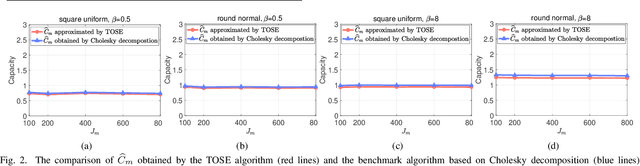
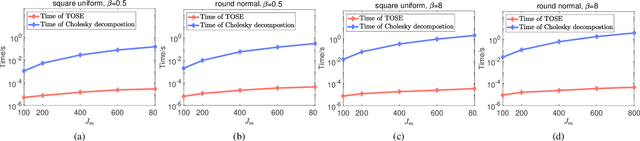
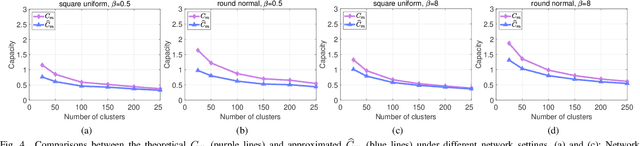
Capacity is one of the most important performance metrics for wireless communication networks. It describes the maximum rate at which the information can be transmitted of a wireless communication system. To support the growing demand for wireless traffic, wireless networks are becoming more dense and complicated, leading to a higher difficulty to derive the capacity. Unfortunately, most existing methods for the capacity calculation take a polynomial time complexity. This will become unaffordable for future ultra-dense networks, where both the number of base stations (BSs) and the number of users are extremely large. In this paper, we propose a fast algorithm TOSE to estimate the capacity for ultra-dense wireless networks. Based on the spiked model of random matrix theory (RMT), our algorithm can avoid the exact eigenvalue derivations of large dimensional matrices, which are complicated and inevitable in conventional capacity calculation methods. Instead, fast eigenvalue estimations can be realized based on the spike approximations in our TOSE algorithm. Our simulation results show that TOSE is an accurate and fast capacity approximation algorithm. Its estimation error is below 5%, and it runs in linear time, which is much lower than the polynomial time complexity of existing methods. In addition, TOSE has superior generality, since it is independent of the distributions of BSs and users, and the shape of network areas.