TOSE: A Fast Capacity Estimation Algorithm Based on Spike Approximations
Paper and Code
Sep 02, 2022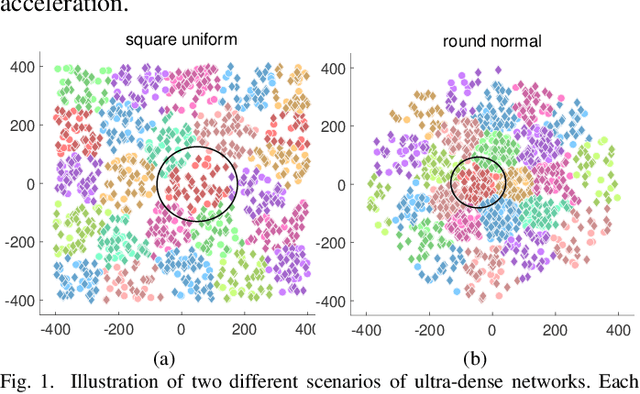
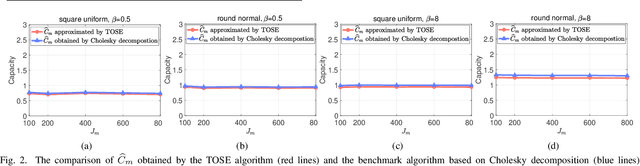
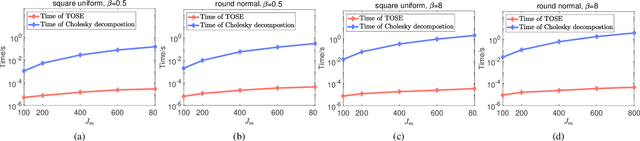
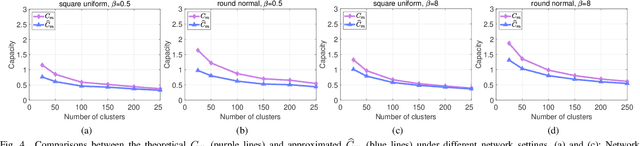
Capacity is one of the most important performance metrics for wireless communication networks. It describes the maximum rate at which the information can be transmitted of a wireless communication system. To support the growing demand for wireless traffic, wireless networks are becoming more dense and complicated, leading to a higher difficulty to derive the capacity. Unfortunately, most existing methods for the capacity calculation take a polynomial time complexity. This will become unaffordable for future ultra-dense networks, where both the number of base stations (BSs) and the number of users are extremely large. In this paper, we propose a fast algorithm TOSE to estimate the capacity for ultra-dense wireless networks. Based on the spiked model of random matrix theory (RMT), our algorithm can avoid the exact eigenvalue derivations of large dimensional matrices, which are complicated and inevitable in conventional capacity calculation methods. Instead, fast eigenvalue estimations can be realized based on the spike approximations in our TOSE algorithm. Our simulation results show that TOSE is an accurate and fast capacity approximation algorithm. Its estimation error is below 5%, and it runs in linear time, which is much lower than the polynomial time complexity of existing methods. In addition, TOSE has superior generality, since it is independent of the distributions of BSs and users, and the shape of network areas.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge