Enhancing LMMSE Performance with Modest Complexity Increase via Neural Network Equalizers

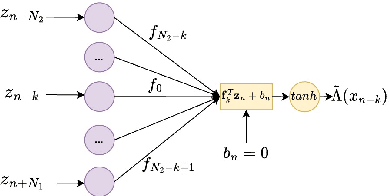
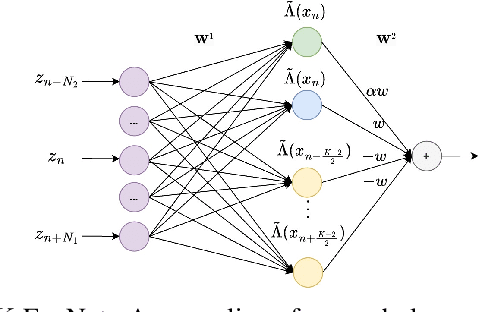
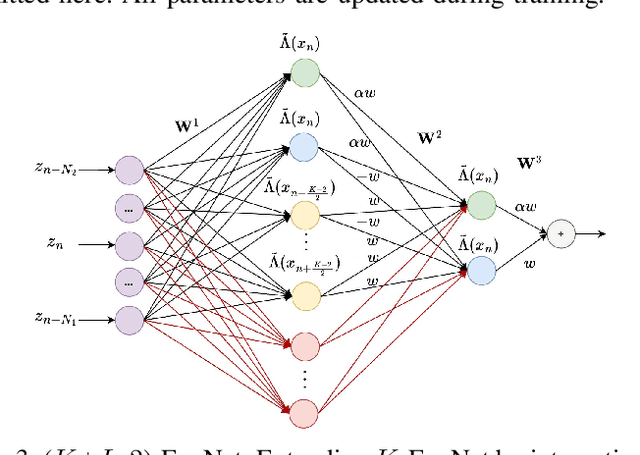
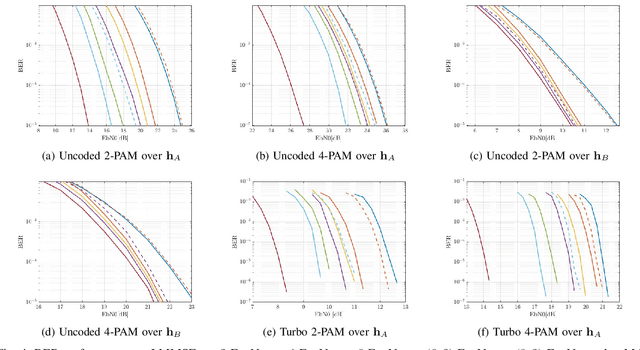
The BCJR algorithm is renowned for its optimal equalization, minimizing bit error rate (BER) over intersymbol interference (ISI) channels. However, its complexity grows exponentially with the channel memory, posing a significant computational burden. In contrast, the linear minimum mean square error (LMMSE) equalizer offers a notably simpler solution, albeit with reduced performance compared to the BCJR. Recently, Neural Network (NN) based equalizers have emerged as promising alternatives. Trained to map observations to the original transmitted symbols, these NNs demonstrate performance similar to the BCJR algorithm. However, they often entail a high number of learnable parameters, resulting in complexities comparable to or even larger than the BCJR. This paper explores the potential of NN-based equalization with a reduced number of learnable parameters and low complexity. We introduce a NN equalizer with complexity comparable to LMMSE, surpassing LMMSE performance and achieving a modest performance gap from the BCJR equalizer. A significant challenge with NNs featuring a limited parameter count is their susceptibility to converging to local minima, leading to suboptimal performance. To address this challenge, we propose a novel NN equalizer architecture with a unique initialization approach based on LMMSE. This innovative method effectively overcomes optimization challenges and enhances LMMSE performance, applicable both with and without turbo decoding.

Source Localization of an Unknown Transmission in Dense Multipath Environments

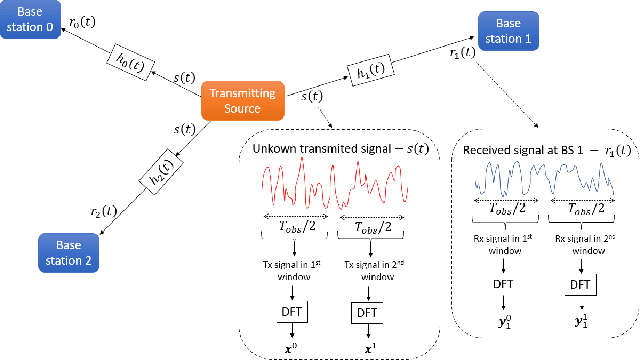
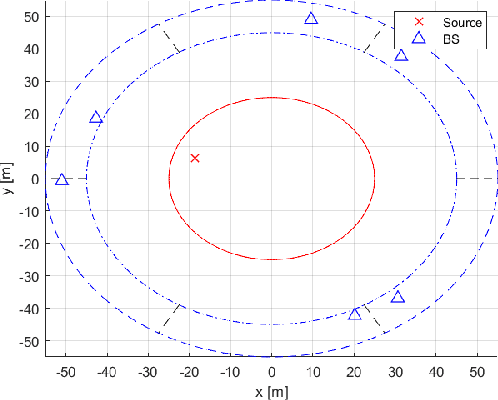
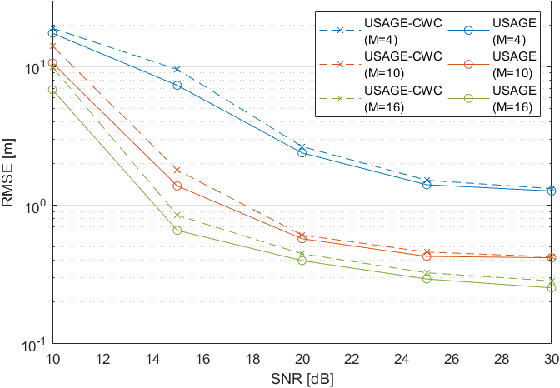
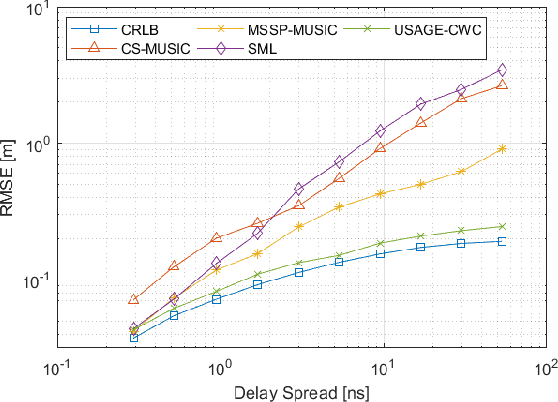
Accurately estimating the position of a wireless emitter in a multipath environment based on samples received at various base stations (in known locations) has been extensively explored in the literature. Existing approaches often assume that the emitted signal is known to the location system, while in some applications, such as locating surveillance or intelligence systems, it usually remains unknown. In this paper, we propose a novel estimator for determining the position of an emitter transmitting an unknown signal in a dense multipath environment with a given power-delay profile. We also derive the Carmer-Rao lower bound (CRLB) to evaluate the estimator's performance. Our approach is based on approximating the dense multipath channel in the frequency domain as a Gaussian random vector using the central limit theorem, formulating a log-likelihood cost function for the position and some features of the transmitted signal, and applying a maximum search over both. The optimization problem is non-convex and has no known analytical solutions, which makes it computationally infeasible for multidimensional brute-force search. To address this challenge, we developed a practical optimization algorithm that overcomes the computational complexity, using reasonable approximations, that provides a feasible position estimator. Through extensive evaluations, we demonstrate that the proposed estimator outperforms other state-of-the-art estimators. Moreover, as the number of base stations and SNR increase, our estimator approaches the CRLB, indicating its effectiveness and efficiency.