Enhancing LMMSE Performance with Modest Complexity Increase via Neural Network Equalizers

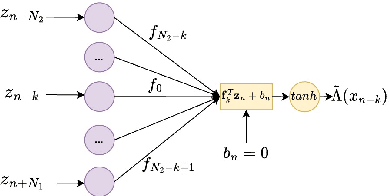
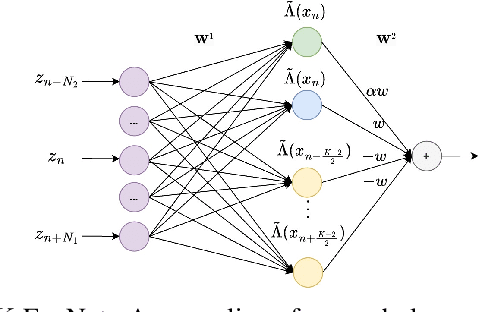
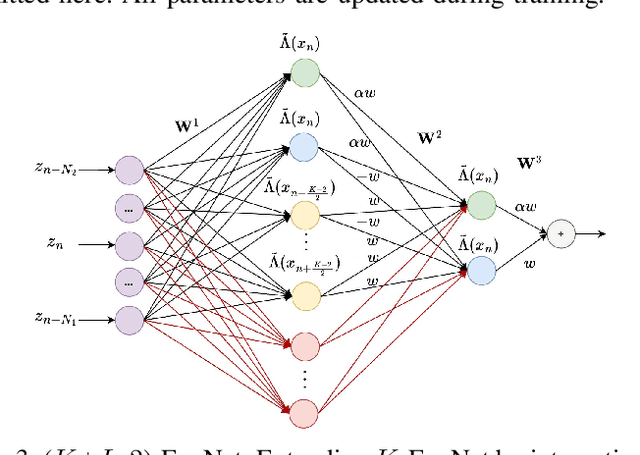
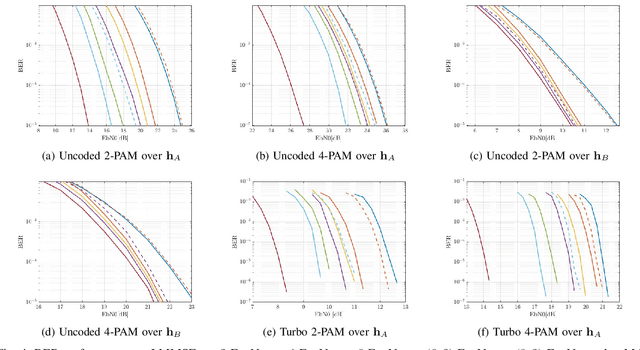
The BCJR algorithm is renowned for its optimal equalization, minimizing bit error rate (BER) over intersymbol interference (ISI) channels. However, its complexity grows exponentially with the channel memory, posing a significant computational burden. In contrast, the linear minimum mean square error (LMMSE) equalizer offers a notably simpler solution, albeit with reduced performance compared to the BCJR. Recently, Neural Network (NN) based equalizers have emerged as promising alternatives. Trained to map observations to the original transmitted symbols, these NNs demonstrate performance similar to the BCJR algorithm. However, they often entail a high number of learnable parameters, resulting in complexities comparable to or even larger than the BCJR. This paper explores the potential of NN-based equalization with a reduced number of learnable parameters and low complexity. We introduce a NN equalizer with complexity comparable to LMMSE, surpassing LMMSE performance and achieving a modest performance gap from the BCJR equalizer. A significant challenge with NNs featuring a limited parameter count is their susceptibility to converging to local minima, leading to suboptimal performance. To address this challenge, we propose a novel NN equalizer architecture with a unique initialization approach based on LMMSE. This innovative method effectively overcomes optimization challenges and enhances LMMSE performance, applicable both with and without turbo decoding.

Conformal Prediction for Manifold-based Source Localization with Gaussian Processes

We tackle the challenge of uncertainty quantification in the localization of a sound source within adverse acoustic environments. Estimating the position of the source is influenced by various factors such as noise and reverberation, leading to significant uncertainty. Quantifying this uncertainty is essential, particularly when localization outcomes impact critical decision-making processes, such as in robot audition, where the accuracy of location estimates directly influences subsequent actions. Despite this, many localization methods typically offer point estimates without quantifying the estimation uncertainty. To address this, we employ conformal prediction (CP)-a framework that delivers statistically valid prediction intervals with finite-sample guarantees, independent of the data distribution. However, commonly used Inductive CP (ICP) methods require a substantial amount of labeled data, which can be difficult to obtain in the localization setting. To mitigate this limitation, we incorporate a manifold-based localization method using Gaussian process regression (GPR), with an efficient Transductive CP (TCP) technique specifically designed for GPR. We demonstrate that our method generates statistically valid uncertainty intervals across different acoustic conditions.