Source Localization of an Unknown Transmission in Dense Multipath Environments
Paper and Code
Oct 13, 2024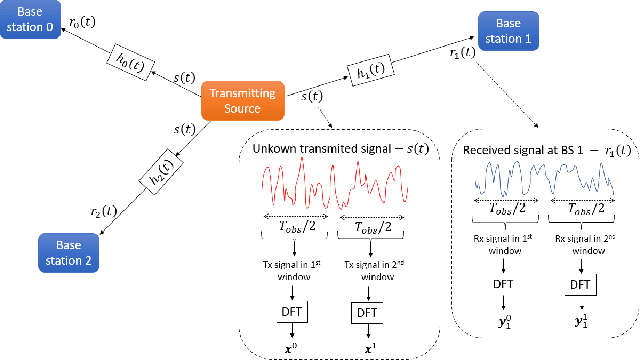
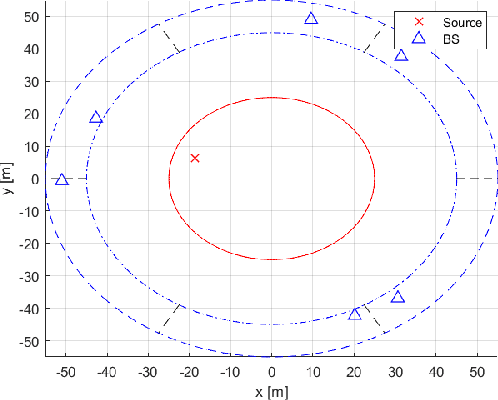
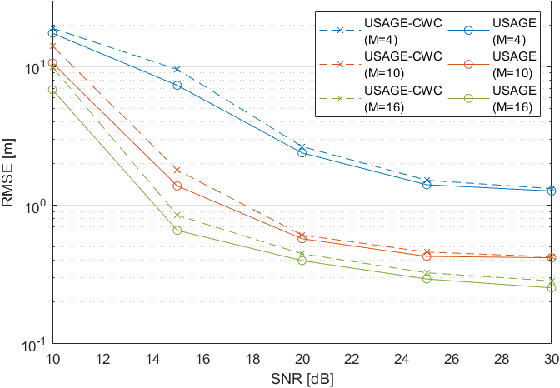
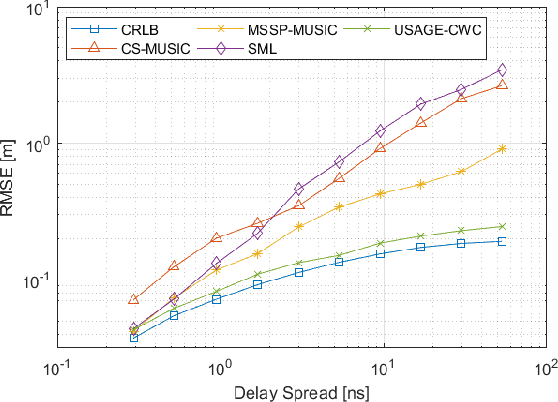
Accurately estimating the position of a wireless emitter in a multipath environment based on samples received at various base stations (in known locations) has been extensively explored in the literature. Existing approaches often assume that the emitted signal is known to the location system, while in some applications, such as locating surveillance or intelligence systems, it usually remains unknown. In this paper, we propose a novel estimator for determining the position of an emitter transmitting an unknown signal in a dense multipath environment with a given power-delay profile. We also derive the Carmer-Rao lower bound (CRLB) to evaluate the estimator's performance. Our approach is based on approximating the dense multipath channel in the frequency domain as a Gaussian random vector using the central limit theorem, formulating a log-likelihood cost function for the position and some features of the transmitted signal, and applying a maximum search over both. The optimization problem is non-convex and has no known analytical solutions, which makes it computationally infeasible for multidimensional brute-force search. To address this challenge, we developed a practical optimization algorithm that overcomes the computational complexity, using reasonable approximations, that provides a feasible position estimator. Through extensive evaluations, we demonstrate that the proposed estimator outperforms other state-of-the-art estimators. Moreover, as the number of base stations and SNR increase, our estimator approaches the CRLB, indicating its effectiveness and efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge