Sub-linear Regret in Adaptive Model Predictive Control

We consider the problem of adaptive Model Predictive Control (MPC) for uncertain linear-systems with additive disturbances and with state and input constraints. We present STT-MPC (Self-Tuning Tube-based Model Predictive Control), an online algorithm that combines the certainty-equivalence principle and polytopic tubes. Specifically, at any given step, STT-MPC infers the system dynamics using the Least Squares Estimator (LSE), and applies a controller obtained by solving an MPC problem using these estimates. The use of polytopic tubes is so that, despite the uncertainties, state and input constraints are satisfied, and recursive-feasibility and asymptotic stability hold. In this work, we analyze the regret of the algorithm, when compared to an oracle algorithm initially aware of the system dynamics. We establish that the expected regret of STT-MPC does not exceed $O(T^{1/2 + \epsilon})$, where $\epsilon \in (0,1)$ is a design parameter tuning the persistent excitation component of the algorithm. Our result relies on a recently proposed exponential decay of sensitivity property and, to the best of our knowledge, is the first of its kind in this setting. We illustrate the performance of our algorithm using a simple numerical example.

Regret Analysis in Deterministic Reinforcement Learning

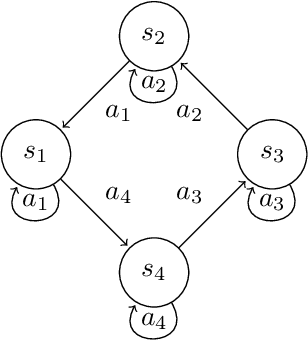
We consider Markov Decision Processes (MDPs) with deterministic transitions and study the problem of regret minimization, which is central to the analysis and design of optimal learning algorithms. We present logarithmic problem-specific regret lower bounds that explicitly depend on the system parameter (in contrast to previous minimax approaches) and thus, truly quantify the fundamental limit of performance achievable by any learning algorithm. Deterministic MDPs can be interpreted as graphs and analyzed in terms of their cycles, a fact which we leverage in order to identify a class of deterministic MDPs whose regret lower bound can be determined numerically. We further exemplify this result on a deterministic line search problem, and a deterministic MDP with state-dependent rewards, whose regret lower bounds we can state explicitly. These bounds share similarities with the known problem-specific bound of the multi-armed bandit problem and suggest that navigation on a deterministic MDP need not have an effect on the performance of a learning algorithm.

Exploration in Structured Reinforcement Learning

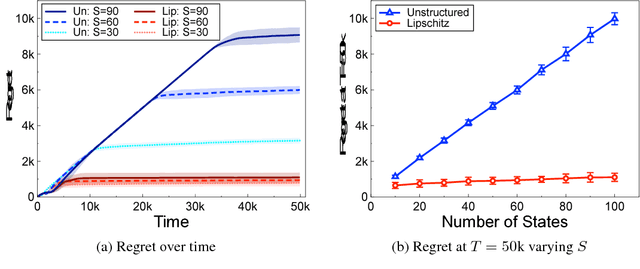
We address reinforcement learning problems with finite state and action spaces where the underlying MDP has some known structure that could be potentially exploited to minimize the exploration of suboptimal (state, action) pairs. For any arbitrary structure, we derive problem-specific regret lower bounds satisfied by any learning algorithm. These lower bounds are made explicit for unstructured MDPs and for those whose transition probabilities and average reward function are Lipschitz continuous w.r.t. the state and action. For Lipschitz MDPs, the bounds are shown not to scale with the sizes $S$ and $A$ of the state and action spaces, i.e., they are smaller than $c \log T$ where $T$ is the time horizon and the constant $c$ only depends on the Lipschitz structure, the span of the bias function, and the minimal action sub-optimality gap. This contrasts with unstructured MDPs where the regret lower bound typically scales as $SA \log T$ . We devise DEL (Directed Exploration Learning), an algorithm that matches our regret lower bounds. We further simplify the algorithm for Lipschitz MDPs, and show that the simplified version is still able to efficiently exploit the structure.