Exploration in Structured Reinforcement Learning

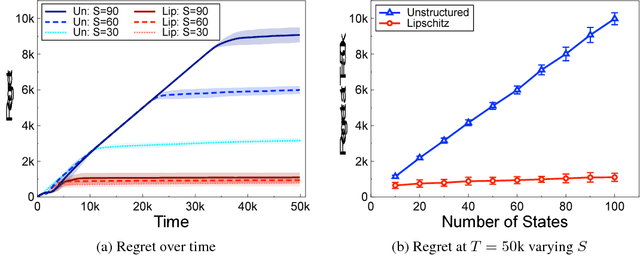
We address reinforcement learning problems with finite state and action spaces where the underlying MDP has some known structure that could be potentially exploited to minimize the exploration of suboptimal (state, action) pairs. For any arbitrary structure, we derive problem-specific regret lower bounds satisfied by any learning algorithm. These lower bounds are made explicit for unstructured MDPs and for those whose transition probabilities and average reward function are Lipschitz continuous w.r.t. the state and action. For Lipschitz MDPs, the bounds are shown not to scale with the sizes $S$ and $A$ of the state and action spaces, i.e., they are smaller than $c \log T$ where $T$ is the time horizon and the constant $c$ only depends on the Lipschitz structure, the span of the bias function, and the minimal action sub-optimality gap. This contrasts with unstructured MDPs where the regret lower bound typically scales as $SA \log T$ . We devise DEL (Directed Exploration Learning), an algorithm that matches our regret lower bounds. We further simplify the algorithm for Lipschitz MDPs, and show that the simplified version is still able to efficiently exploit the structure.