Target alignment in truncated kernel ridge regression

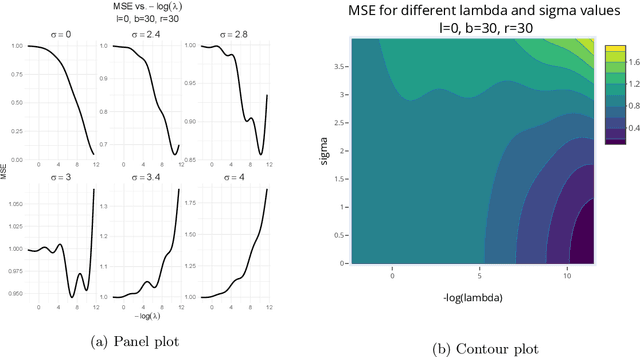
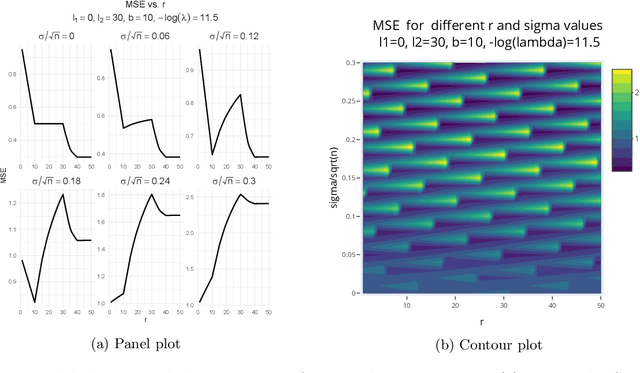
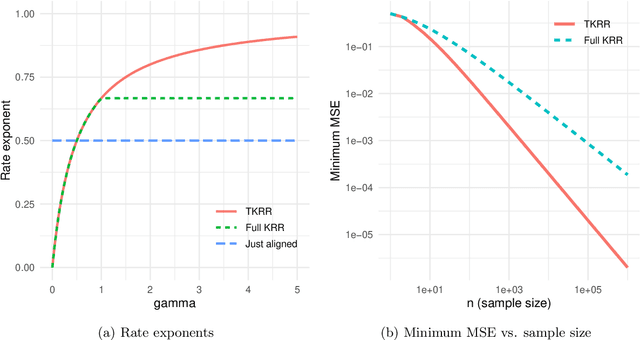
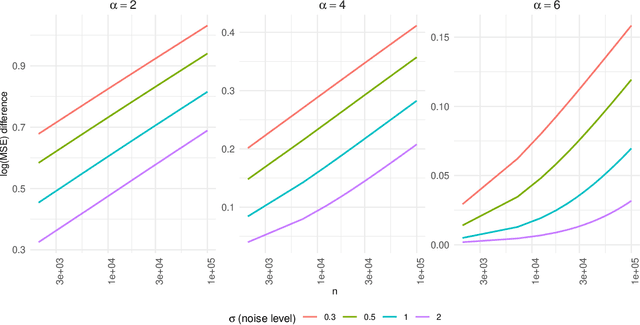
Kernel ridge regression (KRR) has recently attracted renewed interest due to its potential for explaining the transient effects, such as double descent, that emerge during neural network training. In this work, we study how the alignment between the target function and the kernel affects the performance of the KRR. We focus on the truncated KRR (TKRR) which utilizes an additional parameter that controls the spectral truncation of the kernel matrix. We show that for polynomial alignment, there is an \emph{over-aligned} regime, in which TKRR can achieve a faster rate than what is achievable by full KRR. The rate of TKRR can improve all the way to the parametric rate, while that of full KRR is capped at a sub-optimal value. This shows that target alignemnt can be better leveraged by utilizing spectral truncation in kernel methods. We also consider the bandlimited alignment setting and show that the regularization surface of TKRR can exhibit transient effects including multiple descent and non-monotonic behavior. Our results show that there is a strong and quantifable relation between the shape of the \emph{alignment spectrum} and the generalization performance of kernel methods, both in terms of rates and in finite samples.

A Framework for an Assessment of the Kernel-target Alignment in Tree Ensemble Kernel Learning

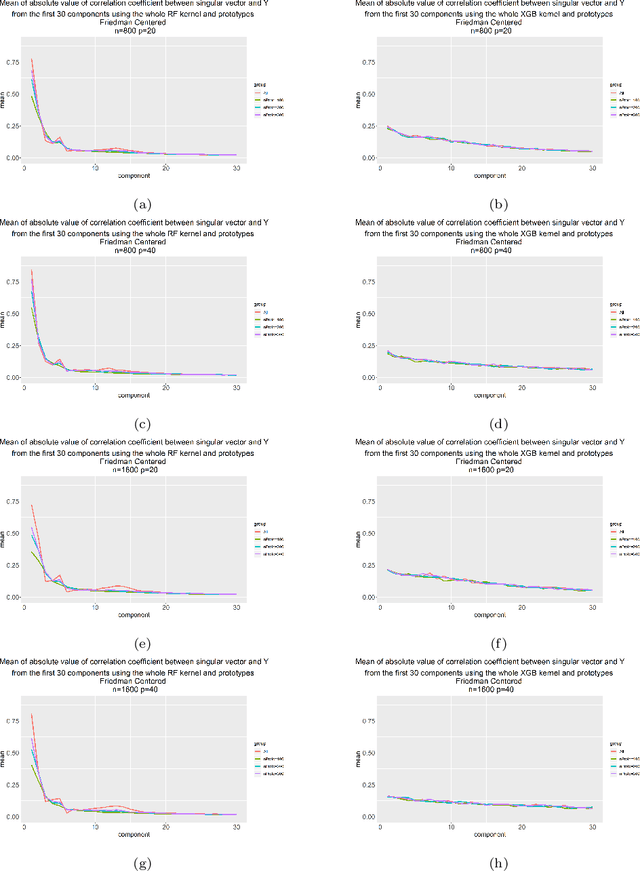
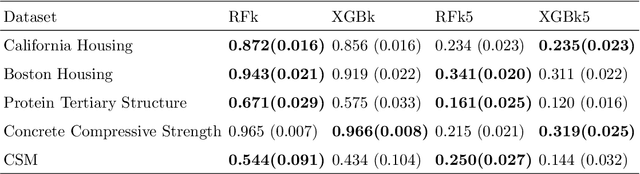
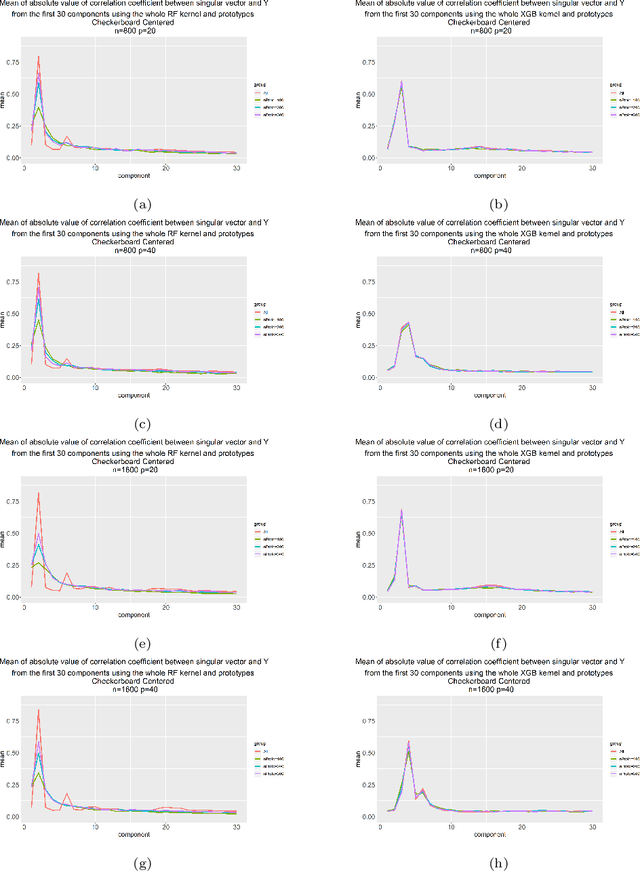
Kernels ensuing from tree ensembles such as random forest (RF) or gradient boosted trees (GBT), when used for kernel learning, have been shown to be competitive to their respective tree ensembles (particularly in higher dimensional scenarios). On the other hand, it has been also shown that performance of the kernel algorithms depends on the degree of the kernel-target alignment. However, the kernel-target alignment for kernel learning based on the tree ensembles has not been investigated and filling this gap is the main goal of our work. Using the eigenanalysis of the kernel matrix, we demonstrate that for continuous targets good performance of the tree-based kernel learning is associated with strong kernel-target alignment. Moreover, we show that well performing tree ensemble based kernels are characterized by strong target aligned components that are expressed through scalar products between the eigenvectors of the kernel matrix and the target. This suggests that when tree ensemble based kernel learning is successful, relevant information for the supervised problem is concentrated near lower dimensional manifold spanned by the target aligned components. Persistence of the strong target aligned components in tree ensemble based kernels is further supported by sensitivity analysis via landmark learning. In addition to a comprehensive simulation study, we also provide experimental results from several real life data sets that are in line with the simulations.

BDNNSurv: Bayesian deep neural networks for survival analysis using pseudo values

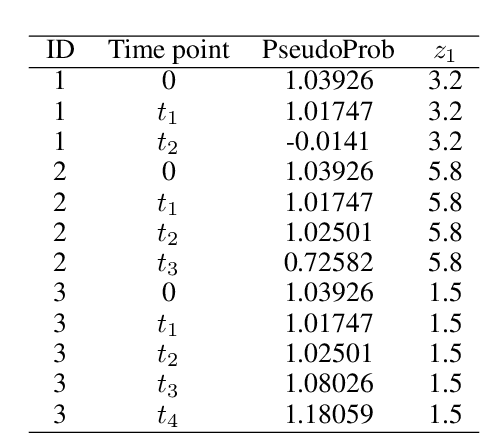
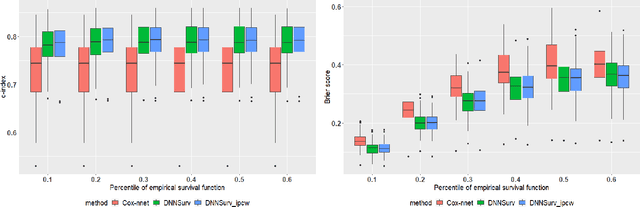
There has been increasing interest in modeling survival data using deep learning methods in medical research. In this paper, we proposed a Bayesian hierarchical deep neural networks model for modeling and prediction of survival data. Compared with previously studied methods, the new proposal can provide not only point estimate of survival probability but also quantification of the corresponding uncertainty, which can be of crucial importance in predictive modeling and subsequent decision making. The favorable statistical properties of point and uncertainty estimates were demonstrated by simulation studies and real data analysis. The Python code implementing the proposed approach was provided.

(Decision and regression) tree ensemble based kernels for regression and classification

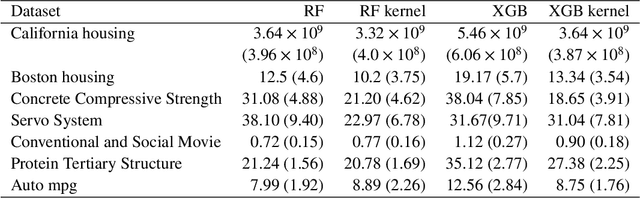
Tree based ensembles such as Breiman's random forest (RF) and Gradient Boosted Trees (GBT) can be interpreted as implicit kernel generators, where the ensuing proximity matrix represents the data-driven tree ensemble kernel. Kernel perspective on the RF has been used to develop a principled framework for theoretical investigation of its statistical properties. Recently, it has been shown that the kernel interpretation is germane to other tree-based ensembles e.g. GBTs. However, practical utility of the links between kernels and the tree ensembles has not been widely explored and systematically evaluated. Focus of our work is investigation of the interplay between kernel methods and the tree based ensembles including the RF and GBT. We elucidate the performance and properties of the RF and GBT based kernels in a comprehensive simulation study comprising of continuous and binary targets. We show that for continuous targets, the RF/GBT kernels are competitive to their respective ensembles in higher dimensional scenarios, particularly in cases with larger number of noisy features. For the binary target, the RF/GBT kernels and their respective ensembles exhibit comparable performance. We provide the results from real life data sets for regression and classification to show how these insights may be leveraged in practice. Overall, our results support the tree ensemble based kernels as a valuable addition to the practitioner's toolbox. Finally, we discuss extensions of the tree ensemble based kernels for survival targets, interpretable prototype and landmarking classification and regression. We outline future line of research for kernels furnished by Bayesian counterparts of the frequentist tree ensembles.

Random Forest (RF) Kernel for Regression, Classification and Survival

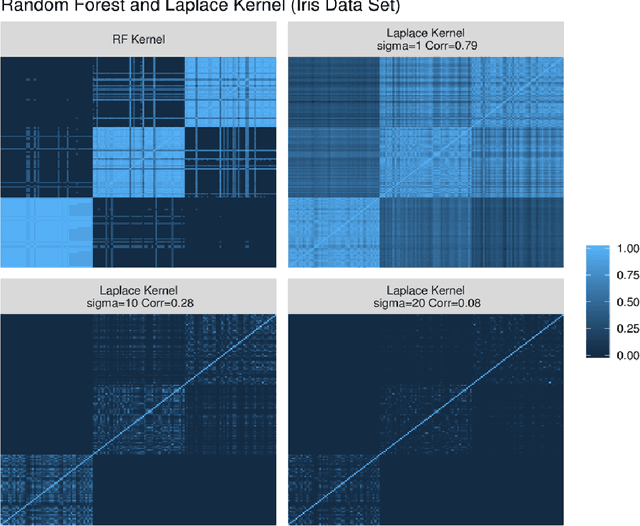
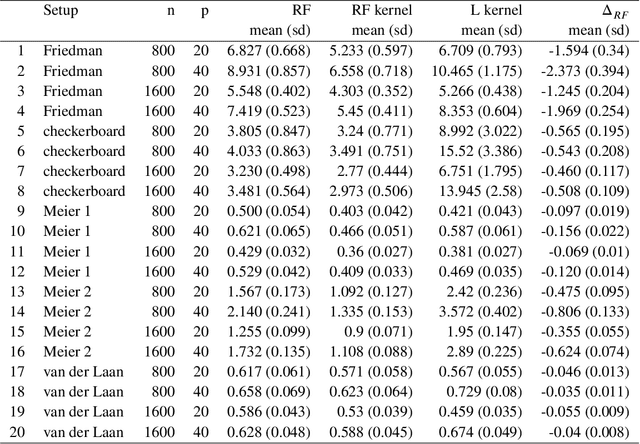
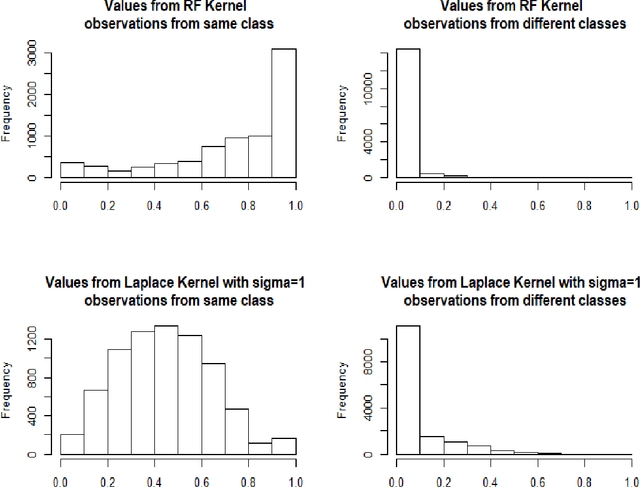
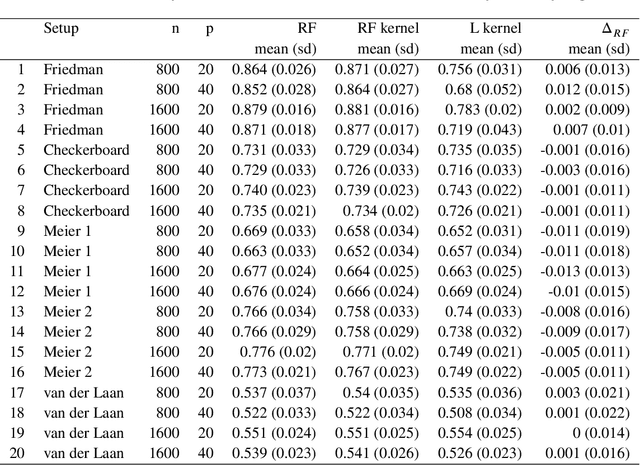
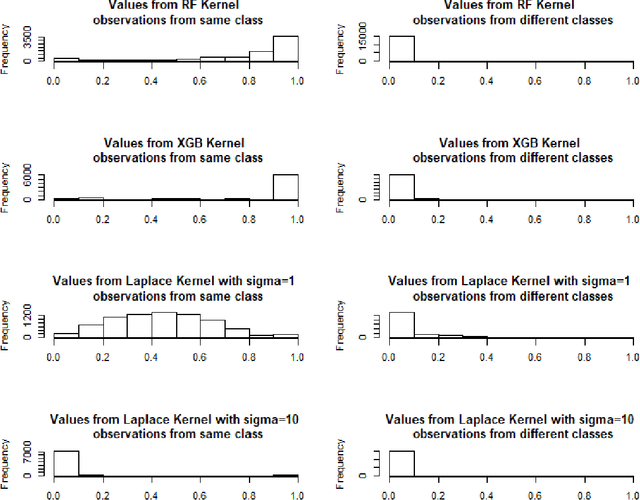
Breiman's random forest (RF) can be interpreted as an implicit kernel generator,where the ensuing proximity matrix represents the data-driven RF kernel. Kernel perspective on the RF has been used to develop a principled framework for theoretical investigation of its statistical properties. However, practical utility of the links between kernels and the RF has not been widely explored and systematically evaluated.Focus of our work is investigation of the interplay between kernel methods and the RF. We elucidate the performance and properties of the data driven RF kernels used by regularized linear models in a comprehensive simulation study comprising of continuous, binary and survival targets. We show that for continuous and survival targets, the RF kernels are competitive to RF in higher dimensional scenarios with larger number of noisy features. For the binary target, the RF kernel and RF exhibit comparable performance. As the RF kernel asymptotically converges to the Laplace kernel, we included it in our evaluation. For most simulation setups, the RF and RFkernel outperformed the Laplace kernel. Nevertheless, in some cases the Laplace kernel was competitive, showing its potential value for applications. We also provide the results from real life data sets for the regression, classification and survival to illustrate how these insights may be leveraged in practice.Finally, we discuss further extensions of the RF kernels in the context of interpretable prototype and landmarking classification, regression and survival. We outline future line of research for kernels furnished by Bayesian counterparts of the RF.

DNNSurv: Deep Neural Networks for Survival Analysis Using Pseudo Values

There has been increasing interest in modelling survival data using deep learning methods in medical research. Current approaches have focused on designing special cost functions to handle censored survival data. We propose a very different method with two steps. In the first step, we transform each subject's survival time into a series of jackknife pseudo conditional survival probabilities and then use these pseudo probabilities as a quantitative response variable in the deep neural network model. By using the pseudo values, we reduce a complex survival analysis to a standard regression problem, which greatly simplifies the neural network construction. Our two-step approach is simple, yet very flexible in making risk predictions for survival data, which is very appealing from the practice point of view. The source code is freely available at http://github.com/lilizhaoUM/DNNSurv.