A Framework for an Assessment of the Kernel-target Alignment in Tree Ensemble Kernel Learning
Paper and Code
Aug 19, 2021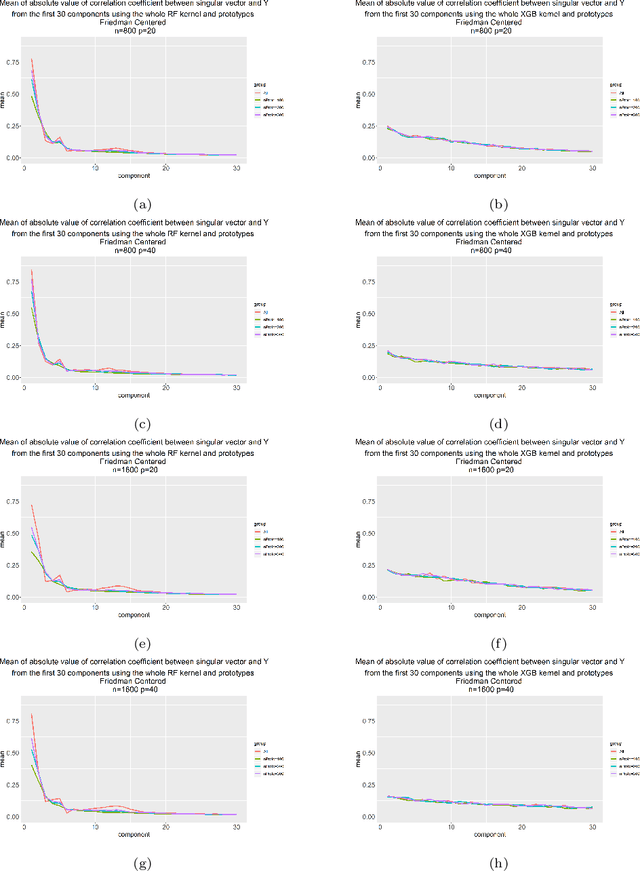
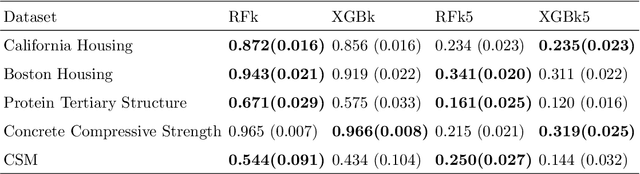
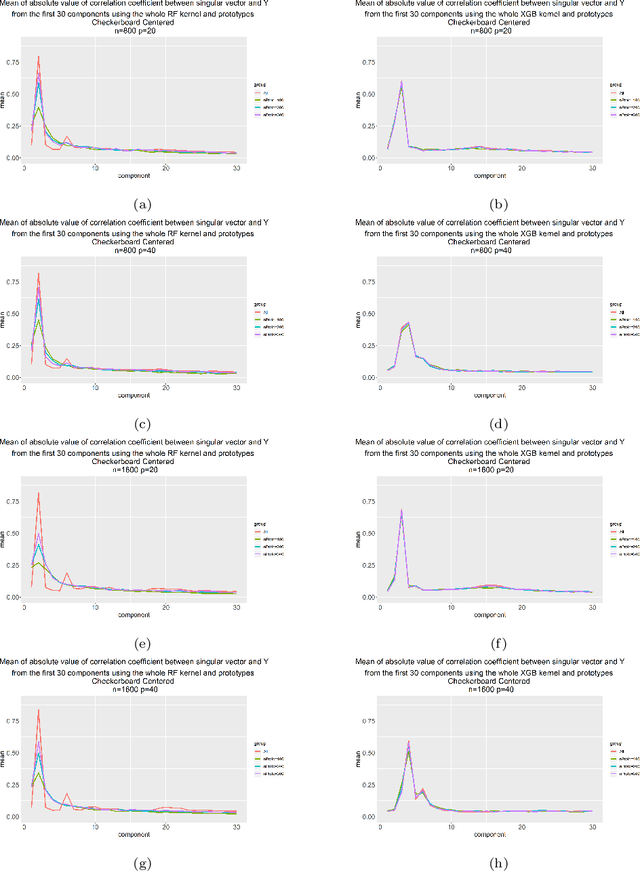
Kernels ensuing from tree ensembles such as random forest (RF) or gradient boosted trees (GBT), when used for kernel learning, have been shown to be competitive to their respective tree ensembles (particularly in higher dimensional scenarios). On the other hand, it has been also shown that performance of the kernel algorithms depends on the degree of the kernel-target alignment. However, the kernel-target alignment for kernel learning based on the tree ensembles has not been investigated and filling this gap is the main goal of our work. Using the eigenanalysis of the kernel matrix, we demonstrate that for continuous targets good performance of the tree-based kernel learning is associated with strong kernel-target alignment. Moreover, we show that well performing tree ensemble based kernels are characterized by strong target aligned components that are expressed through scalar products between the eigenvectors of the kernel matrix and the target. This suggests that when tree ensemble based kernel learning is successful, relevant information for the supervised problem is concentrated near lower dimensional manifold spanned by the target aligned components. Persistence of the strong target aligned components in tree ensemble based kernels is further supported by sensitivity analysis via landmark learning. In addition to a comprehensive simulation study, we also provide experimental results from several real life data sets that are in line with the simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge