Random Forest (RF) Kernel for Regression, Classification and Survival
Paper and Code
Aug 31, 2020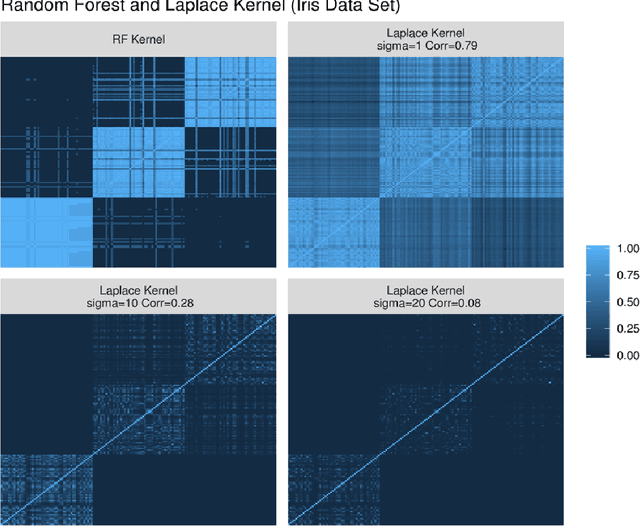
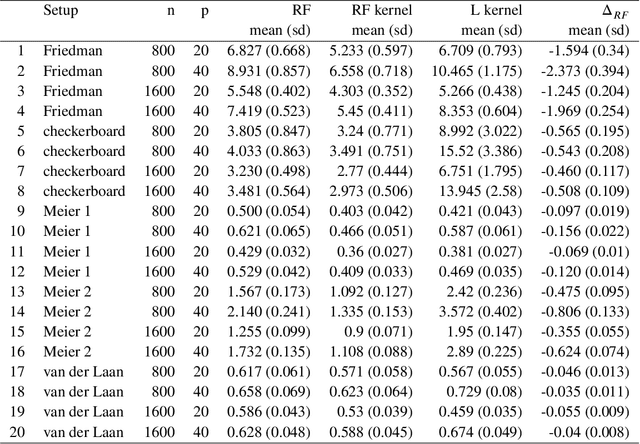
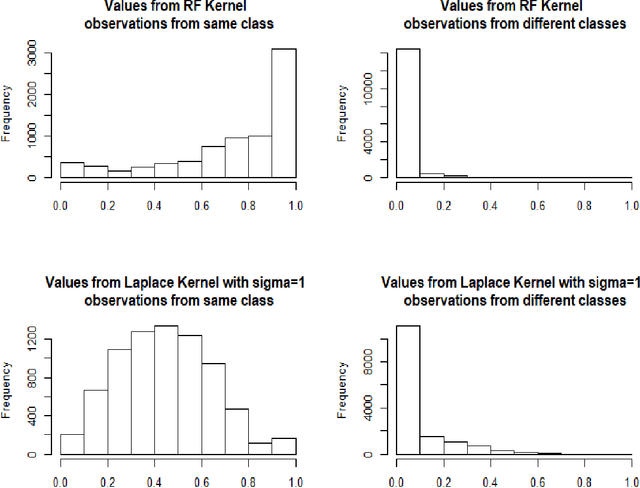
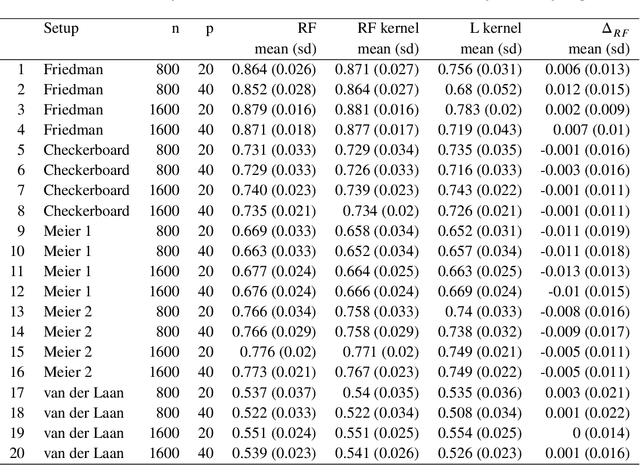
Breiman's random forest (RF) can be interpreted as an implicit kernel generator,where the ensuing proximity matrix represents the data-driven RF kernel. Kernel perspective on the RF has been used to develop a principled framework for theoretical investigation of its statistical properties. However, practical utility of the links between kernels and the RF has not been widely explored and systematically evaluated.Focus of our work is investigation of the interplay between kernel methods and the RF. We elucidate the performance and properties of the data driven RF kernels used by regularized linear models in a comprehensive simulation study comprising of continuous, binary and survival targets. We show that for continuous and survival targets, the RF kernels are competitive to RF in higher dimensional scenarios with larger number of noisy features. For the binary target, the RF kernel and RF exhibit comparable performance. As the RF kernel asymptotically converges to the Laplace kernel, we included it in our evaluation. For most simulation setups, the RF and RFkernel outperformed the Laplace kernel. Nevertheless, in some cases the Laplace kernel was competitive, showing its potential value for applications. We also provide the results from real life data sets for the regression, classification and survival to illustrate how these insights may be leveraged in practice.Finally, we discuss further extensions of the RF kernels in the context of interpretable prototype and landmarking classification, regression and survival. We outline future line of research for kernels furnished by Bayesian counterparts of the RF.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge