General Intelligent Imaging and Uncertainty Quantification by Deterministic Diffusion Model

Computational imaging is crucial in many disciplines from autonomous driving to life sciences. However, traditional model-driven and iterative methods consume large computational power and lack scalability for imaging. Deep learning (DL) is effective in processing local-to-local patterns, but it struggles with handling universal global-to-local (nonlocal) patterns under current frameworks. To bridge this gap, we propose a novel DL framework that employs a progressive denoising strategy, named the deterministic diffusion model (DDM), to facilitate general computational imaging at a low cost. We experimentally demonstrate the efficient and faithful image reconstruction capabilities of DDM from nonlocal patterns, such as speckles from multimode fiber and intensity patterns of second harmonic generation, surpassing the capability of previous state-of-the-art DL algorithms. By embedding Bayesian inference into DDM, we establish a theoretical framework and provide experimental proof of its uncertainty quantification. This advancement ensures the predictive reliability of DDM, avoiding misjudgment in high-stakes scenarios. This versatile and integrable DDM framework can readily extend and improve the efficacy of existing DL-based imaging applications.

Recognizing three-dimensional phase images with deep learning

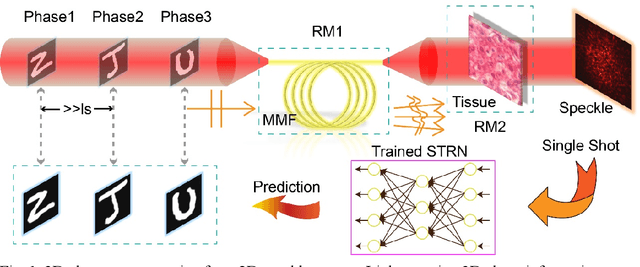
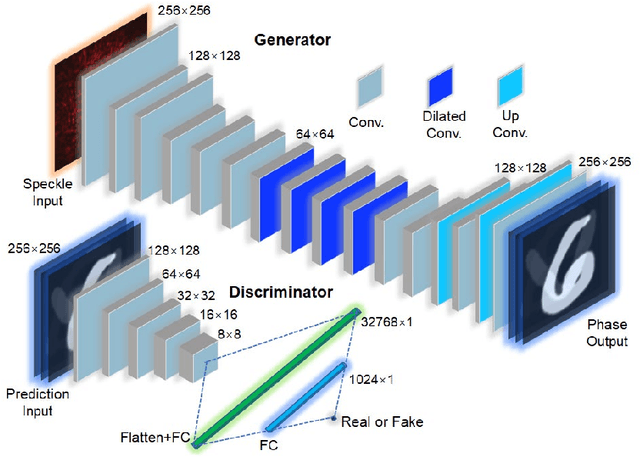
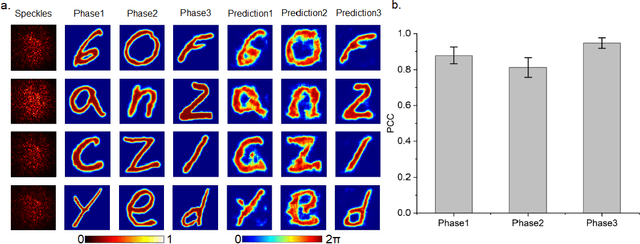
Optical phase contains key information for biomedical and astronomical imaging. However, it is often obscured by layers of heterogeneous and scattering media, which render optical phase imaging at different depths an utmost challenge. Limited by the memory effect, current methods for phase imaging in strong scattering media are inapplicable to retrieving phases at different depths. To address this challenge, we developed a speckle three-dimensional reconstruction network (STRN) to recognize phase objects behind scattering media, which circumvents the limitations of memory effect. From the single-shot, reference-free and scanning-free speckle pattern input, STRN distinguishes depth-resolving quantitative phase information with high fidelity. Our results promise broad applications in biomedical tomography and endoscopy.

Soft Methodology for Cost-and-error Sensitive Classification

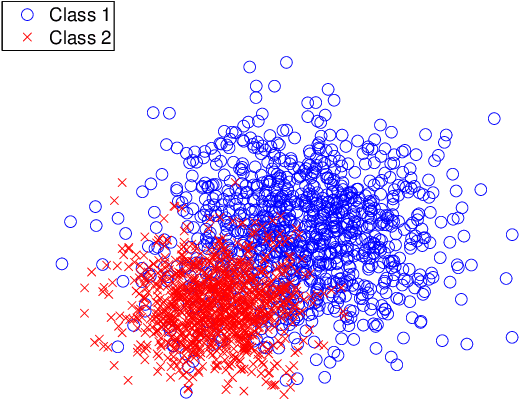
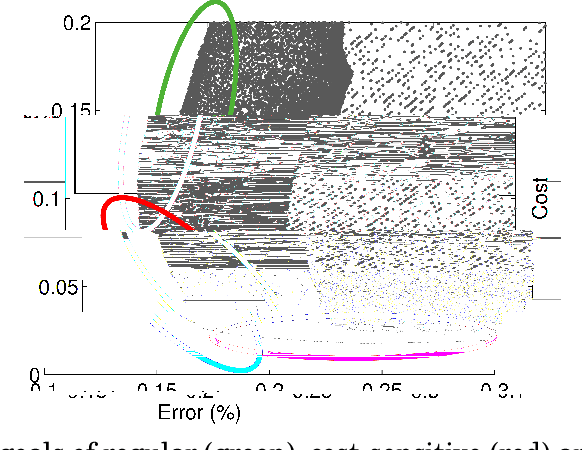
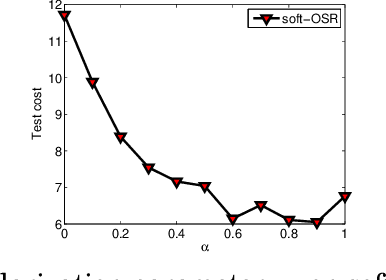
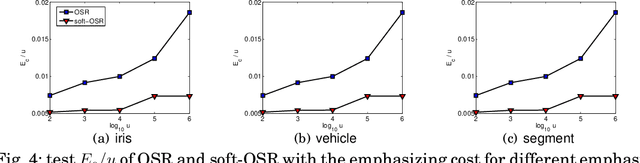
Many real-world data mining applications need varying cost for different types of classification errors and thus call for cost-sensitive classification algorithms. Existing algorithms for cost-sensitive classification are successful in terms of minimizing the cost, but can result in a high error rate as the trade-off. The high error rate holds back the practical use of those algorithms. In this paper, we propose a novel cost-sensitive classification methodology that takes both the cost and the error rate into account. The methodology, called soft cost-sensitive classification, is established from a multicriteria optimization problem of the cost and the error rate, and can be viewed as regularizing cost-sensitive classification with the error rate. The simple methodology allows immediate improvements of existing cost-sensitive classification algorithms. Experiments on the benchmark and the real-world data sets show that our proposed methodology indeed achieves lower test error rates and similar (sometimes lower) test costs than existing cost-sensitive classification algorithms. We also demonstrate that the methodology can be extended for considering the weighted error rate instead of the original error rate. This extension is useful for tackling unbalanced classification problems.