TSCI: two stage curvature identification for causal inference with invalid instruments

TSCI implements treatment effect estimation from observational data under invalid instruments in the R statistical computing environment. Existing instrumental variable approaches rely on arguably strong and untestable identification assumptions, which limits their practical application. TSCI does not require the classical instrumental variable identification conditions and is effective even if all instruments are invalid. TSCI implements a two-stage algorithm. In the first stage, machine learning is used to cope with nonlinearities and interactions in the treatment model. In the second stage, a space to capture the instrument violations is selected in a data-adaptive way. These violations are then projected out to estimate the treatment effect.

Confidence and Uncertainty Assessment for Distributional Random Forests

The Distributional Random Forest (DRF) is a recently introduced Random Forest algorithm to estimate multivariate conditional distributions. Due to its general estimation procedure, it can be employed to estimate a wide range of targets such as conditional average treatment effects, conditional quantiles, and conditional correlations. However, only results about the consistency and convergence rate of the DRF prediction are available so far. We characterize the asymptotic distribution of DRF and develop a bootstrap approximation of it. This allows us to derive inferential tools for quantifying standard errors and the construction of confidence regions that have asymptotic coverage guarantees. In simulation studies, we empirically validate the developed theory for inference of low-dimensional targets and for testing distributional differences between two populations.

Treatment Effect Estimation from Observational Network Data using Augmented Inverse Probability Weighting and Machine Learning

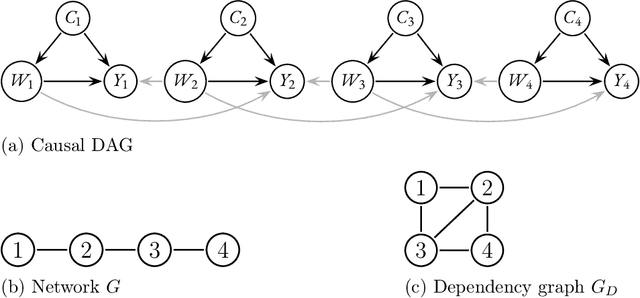
Causal inference methods for treatment effect estimation usually assume independent experimental units. However, this assumption is often questionable because experimental units may interact. We develop augmented inverse probability weighting (AIPW) for estimation and inference of causal treatment effects on dependent observational data. Our framework covers very general cases of spillover effects induced by units interacting in networks. We use plugin machine learning to estimate infinite-dimensional nuisance components leading to a consistent treatment effect estimator that converges at the parametric rate and asymptotically follows a Gaussian distribution.

Double Machine Learning for Partially Linear Mixed-Effects Models with Repeated Measurements

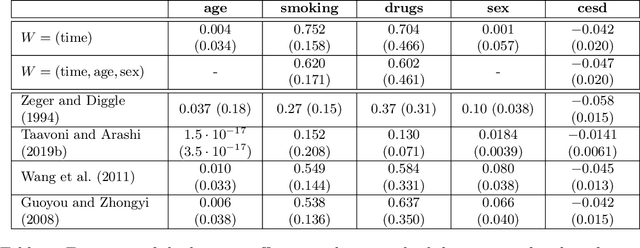
Traditionally, spline or kernel approaches in combination with parametric estimation are used to infer the linear coefficient (fixed effects) in a partially linear mixed-effects model (PLMM) for repeated measurements. Using machine learning algorithms allows us to incorporate more complex interaction structures and high-dimensional variables. We employ double machine learning to cope with the nonparametric part of the PLMM: the nonlinear variables are regressed out nonparametrically from both the linear variables and the response. This adjustment can be performed with any machine learning algorithm, for instance random forests. The adjusted variables satisfy a linear mixed-effects model, where the linear coefficient can be estimated with standard linear mixed-effects techniques. We prove that the estimated fixed effects coefficient converges at the parametric rate and is asymptotically Gaussian distributed and semiparametrically efficient. Empirical examples demonstrate our proposed algorithm. We present two simulation studies and analyze a dataset with repeated CD4 cell counts from HIV patients. Software code for our method is available in the R-package dmlalg.