Treatment Effect Estimation from Observational Network Data using Augmented Inverse Probability Weighting and Machine Learning
Paper and Code
Jun 29, 2022
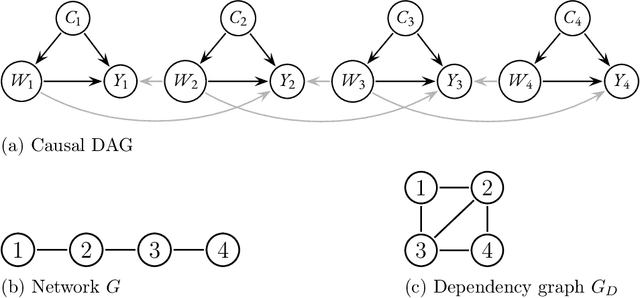


Causal inference methods for treatment effect estimation usually assume independent experimental units. However, this assumption is often questionable because experimental units may interact. We develop augmented inverse probability weighting (AIPW) for estimation and inference of causal treatment effects on dependent observational data. Our framework covers very general cases of spillover effects induced by units interacting in networks. We use plugin machine learning to estimate infinite-dimensional nuisance components leading to a consistent treatment effect estimator that converges at the parametric rate and asymptotically follows a Gaussian distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge