Double Machine Learning for Partially Linear Mixed-Effects Models with Repeated Measurements

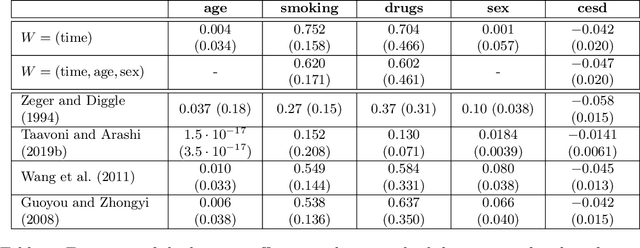
Traditionally, spline or kernel approaches in combination with parametric estimation are used to infer the linear coefficient (fixed effects) in a partially linear mixed-effects model (PLMM) for repeated measurements. Using machine learning algorithms allows us to incorporate more complex interaction structures and high-dimensional variables. We employ double machine learning to cope with the nonparametric part of the PLMM: the nonlinear variables are regressed out nonparametrically from both the linear variables and the response. This adjustment can be performed with any machine learning algorithm, for instance random forests. The adjusted variables satisfy a linear mixed-effects model, where the linear coefficient can be estimated with standard linear mixed-effects techniques. We prove that the estimated fixed effects coefficient converges at the parametric rate and is asymptotically Gaussian distributed and semiparametrically efficient. Empirical examples demonstrate our proposed algorithm. We present two simulation studies and analyze a dataset with repeated CD4 cell counts from HIV patients. Software code for our method is available in the R-package dmlalg.