Conor Rosato
Hess-MC2: Sequential Monte Carlo Squared using Hessian Information and Second Order Proposals
Jul 10, 2025
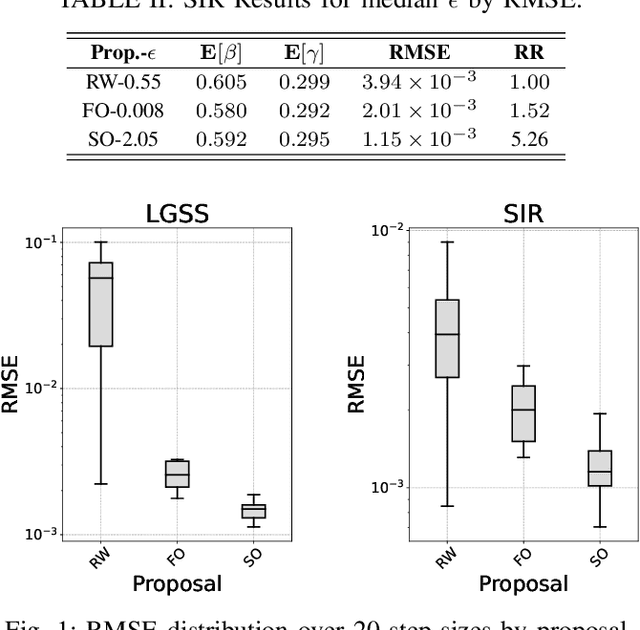
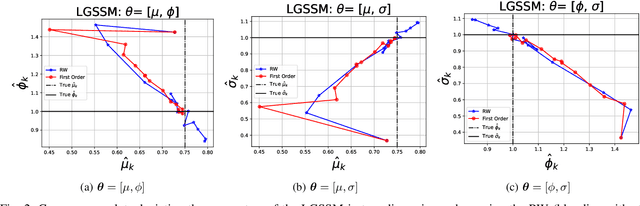
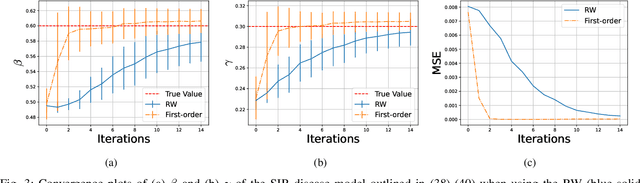
Abstract:When performing Bayesian inference using Sequential Monte Carlo (SMC) methods, two considerations arise: the accuracy of the posterior approximation and computational efficiency. To address computational demands, Sequential Monte Carlo Squared (SMC$^2$) is well-suited for high-performance computing (HPC) environments. The design of the proposal distribution within SMC$^2$ can improve accuracy and exploration of the posterior as poor proposals may lead to high variance in importance weights and particle degeneracy. The Metropolis-Adjusted Langevin Algorithm (MALA) uses gradient information so that particles preferentially explore regions of higher probability. In this paper, we extend this idea by incorporating second-order information, specifically the Hessian of the log-target. While second-order proposals have been explored previously in particle Markov Chain Monte Carlo (p-MCMC) methods, we are the first to introduce them within the SMC$^2$ framework. Second-order proposals not only use the gradient (first-order derivative), but also the curvature (second-order derivative) of the target distribution. Experimental results on synthetic models highlight the benefits of our approach in terms of step-size selection and posterior approximation accuracy when compared to other proposals.
Efficient MCMC Sampling with Expensive-to-Compute and Irregular Likelihoods
May 15, 2025Abstract:Bayesian inference with Markov Chain Monte Carlo (MCMC) is challenging when the likelihood function is irregular and expensive to compute. We explore several sampling algorithms that make use of subset evaluations to reduce computational overhead. We adapt the subset samplers for this setting where gradient information is not available or is unreliable. To achieve this, we introduce data-driven proxies in place of Taylor expansions and define a novel computation-cost aware adaptive controller. We undertake an extensive evaluation for a challenging disease modelling task and a configurable task with similar irregularity in the likelihood surface. We find our improved version of Hierarchical Importance with Nested Training Samples (HINTS), with adaptive proposals and a data-driven proxy, obtains the best sampling error in a fixed computational budget. We conclude that subset evaluations can provide cheap and naturally-tempered exploration, while a data-driven proxy can pre-screen proposals successfully in explored regions of the state space. These two elements combine through hierarchical delayed acceptance to achieve efficient, exact sampling.
Enhanced SMC$^2$: Leveraging Gradient Information from Differentiable Particle Filters Within Langevin Proposals
Jul 24, 2024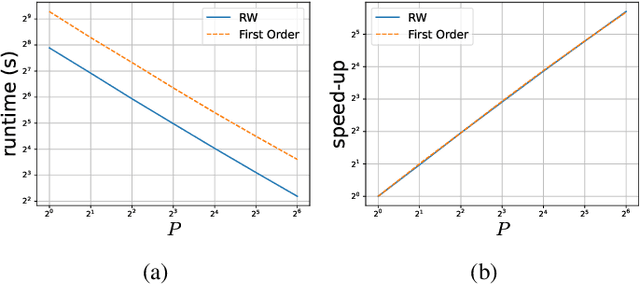
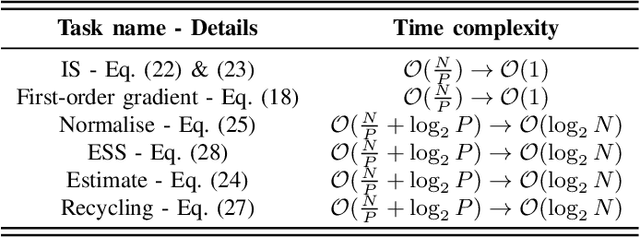
Abstract:Sequential Monte Carlo Squared (SMC$^2$) is a Bayesian method which can infer the states and parameters of non-linear, non-Gaussian state-space models. The standard random-walk proposal in SMC$^2$ faces challenges, particularly with high-dimensional parameter spaces. This study outlines a novel approach by harnessing first-order gradients derived from a Common Random Numbers - Particle Filter (CRN-PF) using PyTorch. The resulting gradients can be leveraged within a Langevin proposal without accept/reject. Including Langevin dynamics within the proposal can result in a higher effective sample size and more accurate parameter estimates when compared with the random-walk. The resulting algorithm is parallelized on distributed memory using Message Passing Interface (MPI) and runs in $\mathcal{O}(\log_2N)$ time complexity. Utilizing 64 computational cores we obtain a 51x speed-up when compared to a single core. A GitHub link is given which provides access to the code.
Efficient Learning of the Parameters of Non-Linear Models using Differentiable Resampling in Particle Filters
Nov 02, 2021



Abstract:It has been widely documented that the sampling and resampling steps in particle filters cannot be differentiated. The {\itshape reparameterisation trick} was introduced to allow the sampling step to be reformulated into a differentiable function. We extend the {\itshape reparameterisation trick} to include the stochastic input to resampling therefore limiting the discontinuities in the gradient calculation after this step. Knowing the gradients of the prior and likelihood allows us to run particle Markov Chain Monte Carlo (p-MCMC) and use the No-U-Turn Sampler (NUTS) as the proposal when estimating parameters. We compare the Metropolis-adjusted Langevin algorithm (MALA), Hamiltonian Monte Carlo with different number of steps and NUTS. We consider two state-space models and show that NUTS improves the mixing of the Markov chain and can produce more accurate results in less computational time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge