Utilising Gradient-Based Proposals Within Sequential Monte Carlo Samplers for Training of Partial Bayesian Neural Networks

Partial Bayesian neural networks (pBNNs) have been shown to perform competitively with fully Bayesian neural networks while only having a subset of the parameters be stochastic. Using sequential Monte Carlo (SMC) samplers as the inference method for pBNNs gives a non-parametric probabilistic estimation of the stochastic parameters, and has shown improved performance over parametric methods. In this paper we introduce a new SMC-based training method for pBNNs by utilising a guided proposal and incorporating gradient-based Markov kernels, which gives us better scalability on high dimensional problems. We show that our new method outperforms the state-of-the-art in terms of predictive performance and optimal loss. We also show that pBNNs scale well with larger batch sizes, resulting in significantly reduced training times and often better performance.

Incorporating the ChEES Criterion into Sequential Monte Carlo Samplers

Markov chain Monte Carlo (MCMC) methods are a powerful but computationally expensive way of performing non-parametric Bayesian inference. MCMC proposals which utilise gradients, such as Hamiltonian Monte Carlo (HMC), can better explore the parameter space of interest if the additional hyper-parameters are chosen well. The No-U-Turn Sampler (NUTS) is a variant of HMC which is extremely effective at selecting these hyper-parameters but is slow to run and is not suited to GPU architectures. An alternative to NUTS, Change in the Estimator of the Expected Square HMC (ChEES-HMC) was shown not only to run faster than NUTS on GPU but also sample from posteriors more efficiently. Sequential Monte Carlo (SMC) samplers are another sampling method which instead output weighted samples from the posterior. They are very amenable to parallelisation and therefore being run on GPUs while having additional flexibility in their choice of proposal over MCMC. We incorporate (ChEEs-HMC) as a proposal into SMC samplers and demonstrate competitive but faster performance than NUTS on a number of tasks.

Enhanced SMC$^2$: Leveraging Gradient Information from Differentiable Particle Filters Within Langevin Proposals

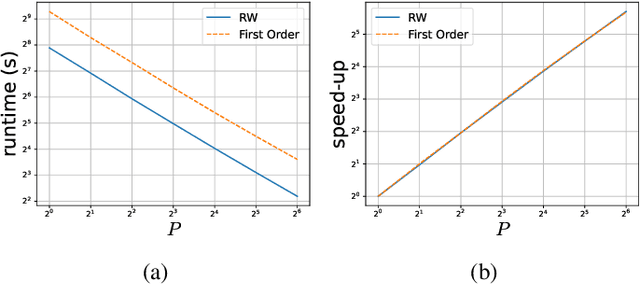
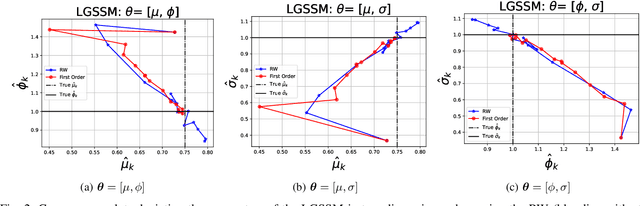
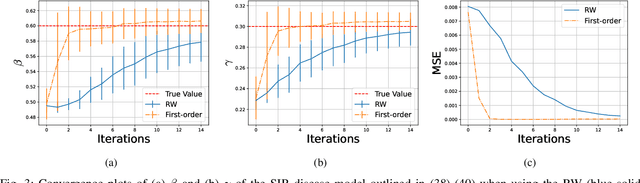
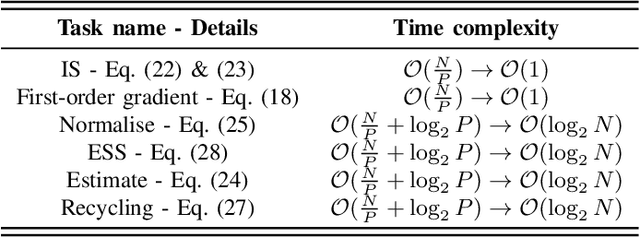
Sequential Monte Carlo Squared (SMC$^2$) is a Bayesian method which can infer the states and parameters of non-linear, non-Gaussian state-space models. The standard random-walk proposal in SMC$^2$ faces challenges, particularly with high-dimensional parameter spaces. This study outlines a novel approach by harnessing first-order gradients derived from a Common Random Numbers - Particle Filter (CRN-PF) using PyTorch. The resulting gradients can be leveraged within a Langevin proposal without accept/reject. Including Langevin dynamics within the proposal can result in a higher effective sample size and more accurate parameter estimates when compared with the random-walk. The resulting algorithm is parallelized on distributed memory using Message Passing Interface (MPI) and runs in $\mathcal{O}(\log_2N)$ time complexity. Utilizing 64 computational cores we obtain a 51x speed-up when compared to a single core. A GitHub link is given which provides access to the code.