Benchmarking the Linear Algebra Awareness of TensorFlow and PyTorch

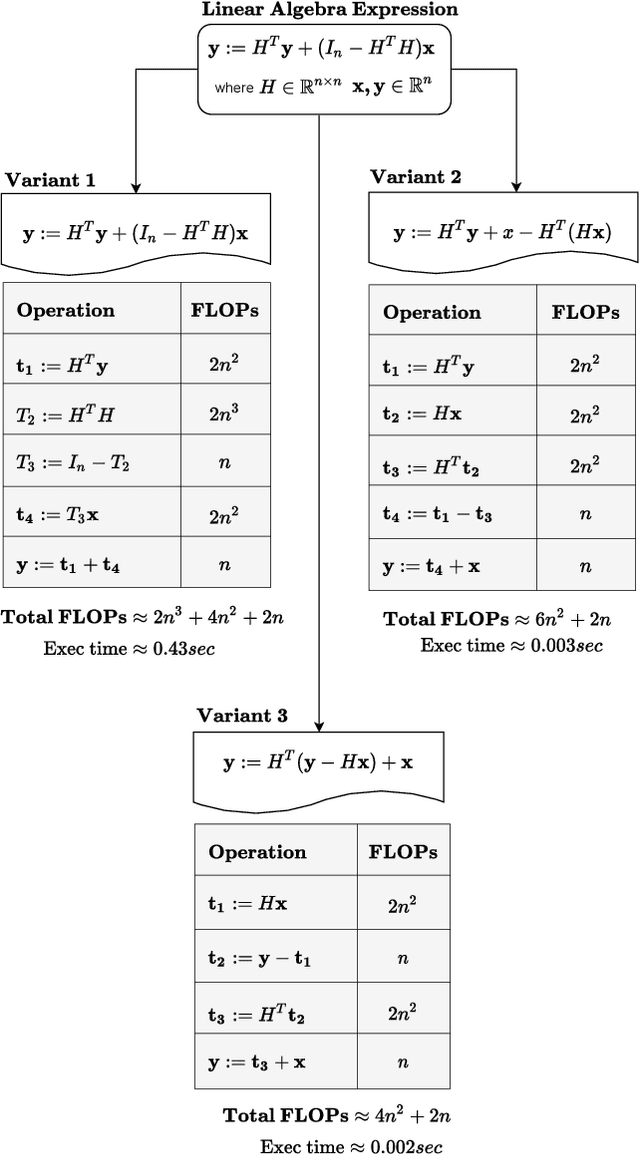
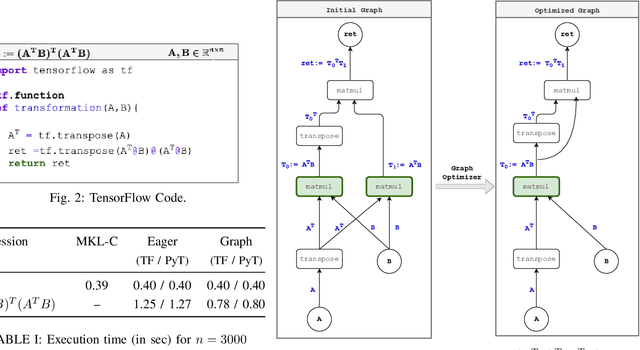
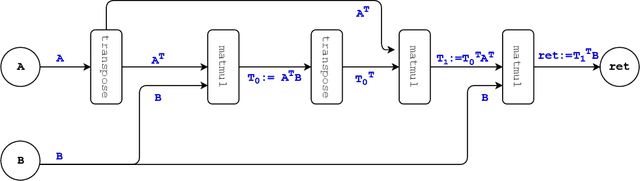
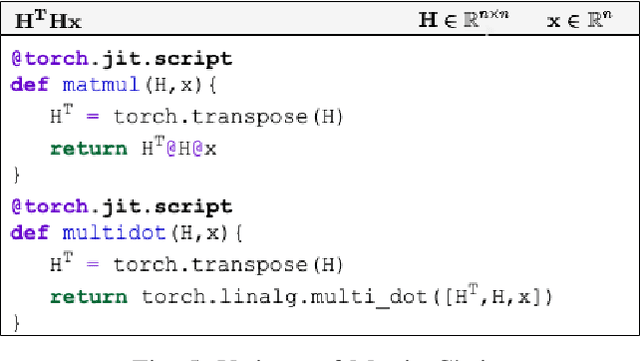
Linear algebra operations, which are ubiquitous in machine learning, form major performance bottlenecks. The High-Performance Computing community invests significant effort in the development of architecture-specific optimized kernels, such as those provided by the BLAS and LAPACK libraries, to speed up linear algebra operations. However, end users are progressively less likely to go through the error prone and time-consuming process of directly using said kernels; instead, frameworks such as TensorFlow (TF) and PyTorch (PyT), which facilitate the development of machine learning applications, are becoming more and more popular. Although such frameworks link to BLAS and LAPACK, it is not clear whether or not they make use of linear algebra knowledge to speed up computations. For this reason, in this paper we develop benchmarks to investigate the linear algebra optimization capabilities of TF and PyT. Our analyses reveal that a number of linear algebra optimizations are still missing; for instance, reducing the number of scalar operations by applying the distributive law, and automatically identifying the optimal parenthesization of a matrix chain. In this work, we focus on linear algebra computations in TF and PyT; we both expose opportunities for performance enhancement to the benefit of the developers of the frameworks and provide end users with guidelines on how to achieve performance gains.

Concurrent Alternating Least Squares for multiple simultaneous Canonical Polyadic Decompositions

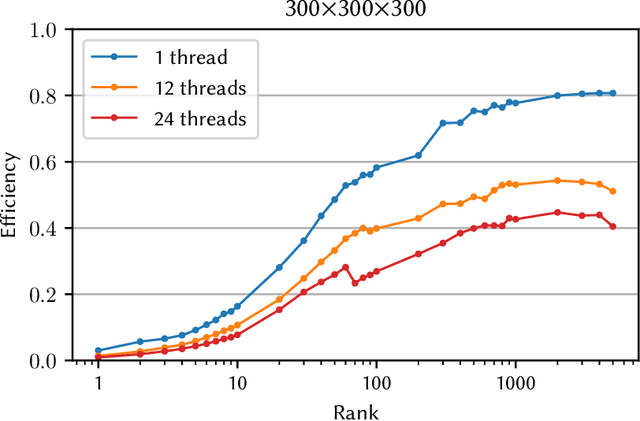
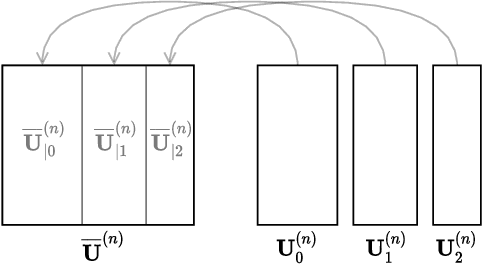
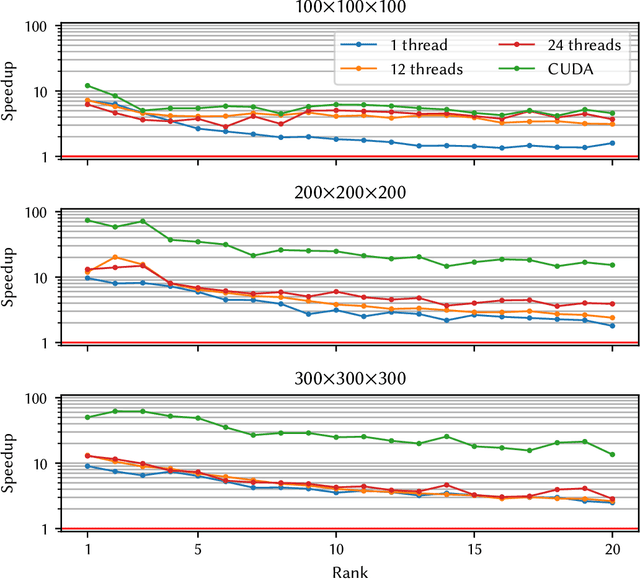
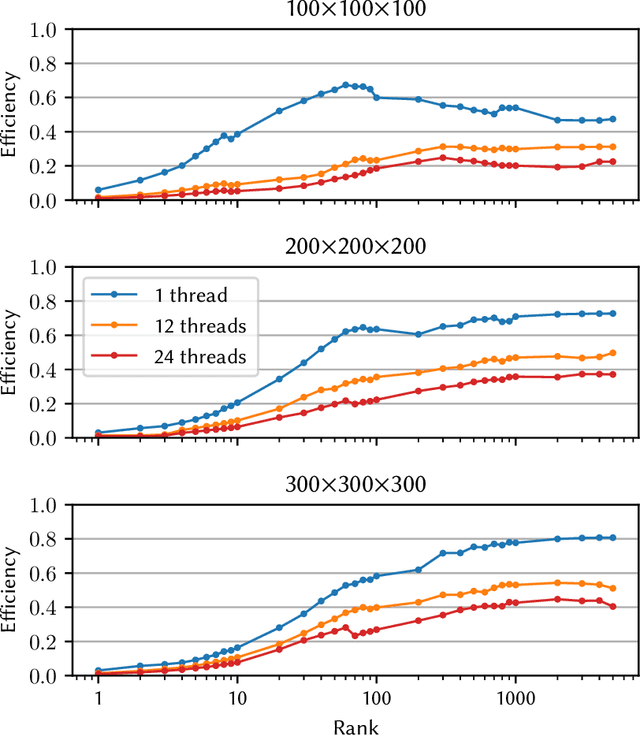
Tensor decompositions, such as CANDECOMP/PARAFAC (CP), are widely used in a variety of applications, such as chemometrics, signal processing, and machine learning. A broadly used method for computing such decompositions relies on the Alternating Least Squares (ALS) algorithm. When the number of components is small, regardless of its implementation, ALS exhibits low arithmetic intensity, which severely hinders its performance and makes GPU offloading ineffective. We observe that, in practice, experts often have to compute multiple decompositions of the same tensor, each with a small number of components (typically fewer than 20), to ultimately find the best ones to use for the application at hand. In this paper, we illustrate how multiple decompositions of the same tensor can be fused together at the algorithmic level to increase the arithmetic intensity. Therefore, it becomes possible to make efficient use of GPUs for further speedups; at the same time the technique is compatible with many enhancements typically used in ALS, such as line search, extrapolation, and non-negativity constraints. We introduce the Concurrent ALS algorithm and library, which offers an interface to Matlab, and a mechanism to effectively deal with the issue that decompositions complete at different times. Experimental results on artificial and real datasets demonstrate a shorter time to completion due to increased arithmetic intensity.