Ranking with Ties based on Noisy Performance Data

We consider the problem of ranking a set of objects based on their performance when the measurement of said performance is subject to noise. In this scenario, the performance is measured repeatedly, resulting in a range of measurements for each object. If the ranges of two objects do not overlap, then we consider one object as 'better' than the other, and we expect it to receive a higher rank; if, however, the ranges overlap, then the objects are incomparable, and we wish them to be assigned the same rank. Unfortunately, the incomparability relation of ranges is in general not transitive; as a consequence, in general the two requirements cannot be satisfied simultaneously, i.e., it is not possible to guarantee both distinct ranks for objects with separated ranges, and same rank for objects with overlapping ranges. This conflict leads to more than one reasonable way to rank a set of objects. In this paper, we explore the ambiguities that arise when ranking with ties, and define a set of reasonable rankings, which we call partial rankings. We develop and analyse three different methodologies to compute a partial ranking. Finally, we show how performance differences among objects can be investigated with the help of partial ranking.

Concurrent Alternating Least Squares for multiple simultaneous Canonical Polyadic Decompositions

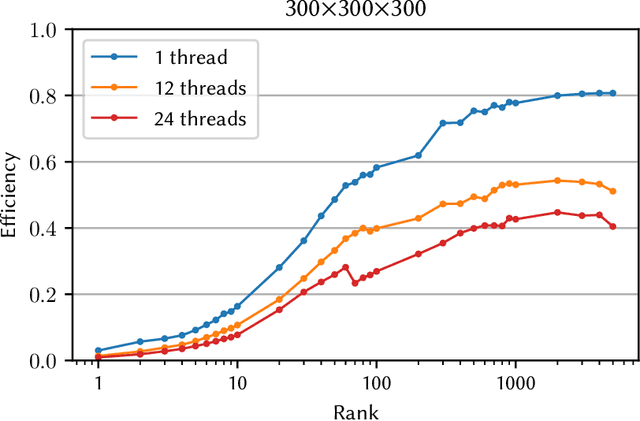
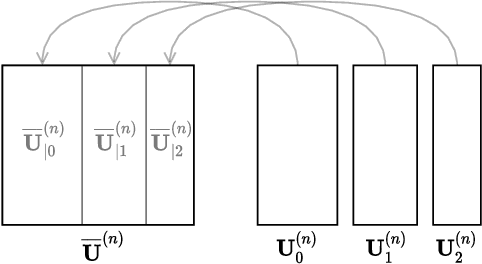
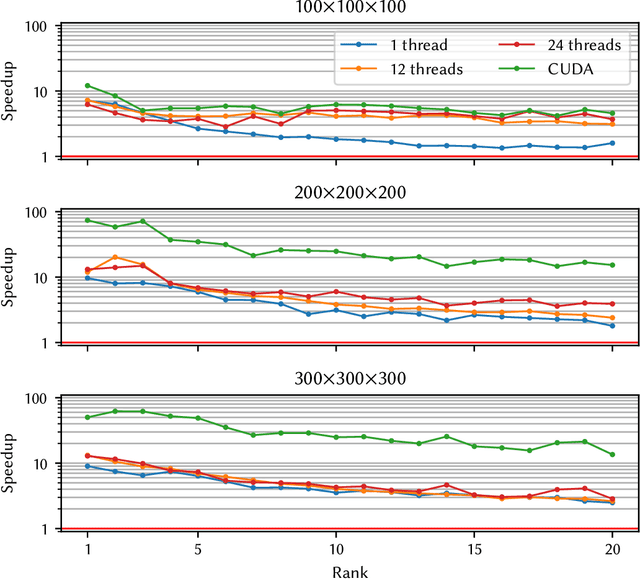
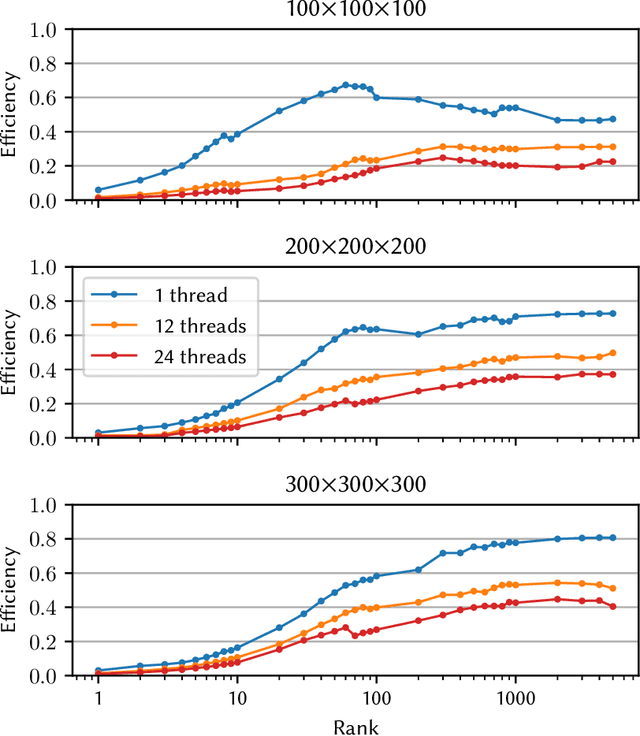
Tensor decompositions, such as CANDECOMP/PARAFAC (CP), are widely used in a variety of applications, such as chemometrics, signal processing, and machine learning. A broadly used method for computing such decompositions relies on the Alternating Least Squares (ALS) algorithm. When the number of components is small, regardless of its implementation, ALS exhibits low arithmetic intensity, which severely hinders its performance and makes GPU offloading ineffective. We observe that, in practice, experts often have to compute multiple decompositions of the same tensor, each with a small number of components (typically fewer than 20), to ultimately find the best ones to use for the application at hand. In this paper, we illustrate how multiple decompositions of the same tensor can be fused together at the algorithmic level to increase the arithmetic intensity. Therefore, it becomes possible to make efficient use of GPUs for further speedups; at the same time the technique is compatible with many enhancements typically used in ALS, such as line search, extrapolation, and non-negativity constraints. We introduce the Concurrent ALS algorithm and library, which offers an interface to Matlab, and a mechanism to effectively deal with the issue that decompositions complete at different times. Experimental results on artificial and real datasets demonstrate a shorter time to completion due to increased arithmetic intensity.