Aravind Sankaran
Ranking with Ties based on Noisy Performance Data
May 28, 2024Abstract:We consider the problem of ranking a set of objects based on their performance when the measurement of said performance is subject to noise. In this scenario, the performance is measured repeatedly, resulting in a range of measurements for each object. If the ranges of two objects do not overlap, then we consider one object as 'better' than the other, and we expect it to receive a higher rank; if, however, the ranges overlap, then the objects are incomparable, and we wish them to be assigned the same rank. Unfortunately, the incomparability relation of ranges is in general not transitive; as a consequence, in general the two requirements cannot be satisfied simultaneously, i.e., it is not possible to guarantee both distinct ranks for objects with separated ranges, and same rank for objects with overlapping ranges. This conflict leads to more than one reasonable way to rank a set of objects. In this paper, we explore the ambiguities that arise when ranking with ties, and define a set of reasonable rankings, which we call partial rankings. We develop and analyse three different methodologies to compute a partial ranking. Finally, we show how performance differences among objects can be investigated with the help of partial ranking.
Benchmarking the Linear Algebra Awareness of TensorFlow and PyTorch
Feb 20, 2022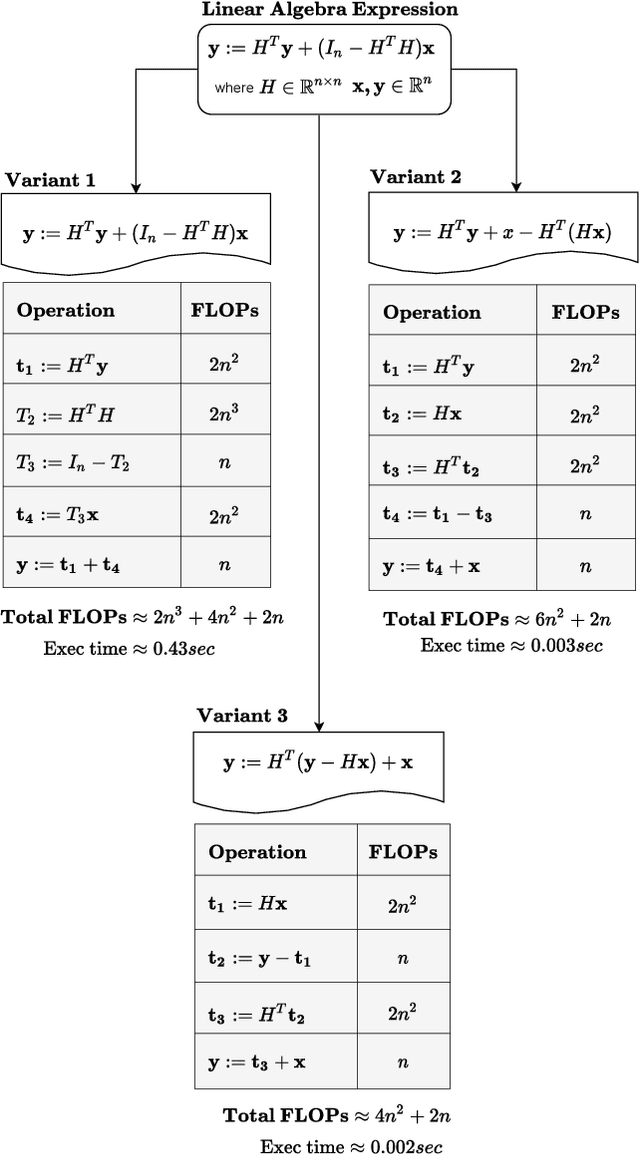
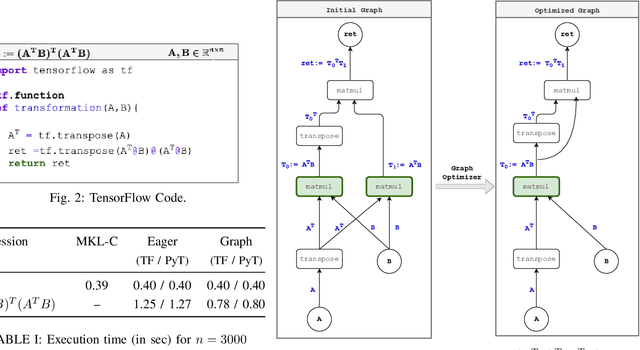
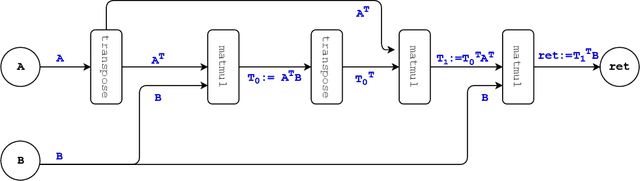
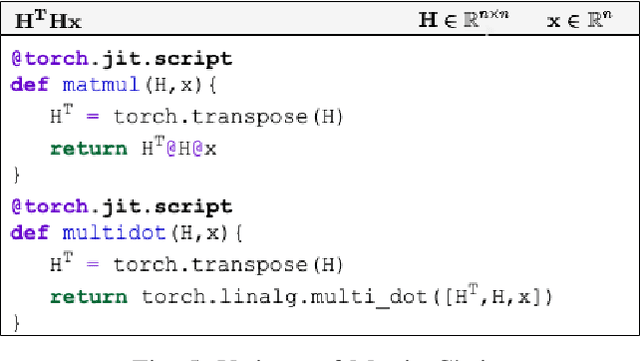
Abstract:Linear algebra operations, which are ubiquitous in machine learning, form major performance bottlenecks. The High-Performance Computing community invests significant effort in the development of architecture-specific optimized kernels, such as those provided by the BLAS and LAPACK libraries, to speed up linear algebra operations. However, end users are progressively less likely to go through the error prone and time-consuming process of directly using said kernels; instead, frameworks such as TensorFlow (TF) and PyTorch (PyT), which facilitate the development of machine learning applications, are becoming more and more popular. Although such frameworks link to BLAS and LAPACK, it is not clear whether or not they make use of linear algebra knowledge to speed up computations. For this reason, in this paper we develop benchmarks to investigate the linear algebra optimization capabilities of TF and PyT. Our analyses reveal that a number of linear algebra optimizations are still missing; for instance, reducing the number of scalar operations by applying the distributive law, and automatically identifying the optimal parenthesization of a matrix chain. In this work, we focus on linear algebra computations in TF and PyT; we both expose opportunities for performance enhancement to the benefit of the developers of the frameworks and provide end users with guidelines on how to achieve performance gains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge