Benchmarking the Linear Algebra Awareness of TensorFlow and PyTorch
Paper and Code
Feb 20, 2022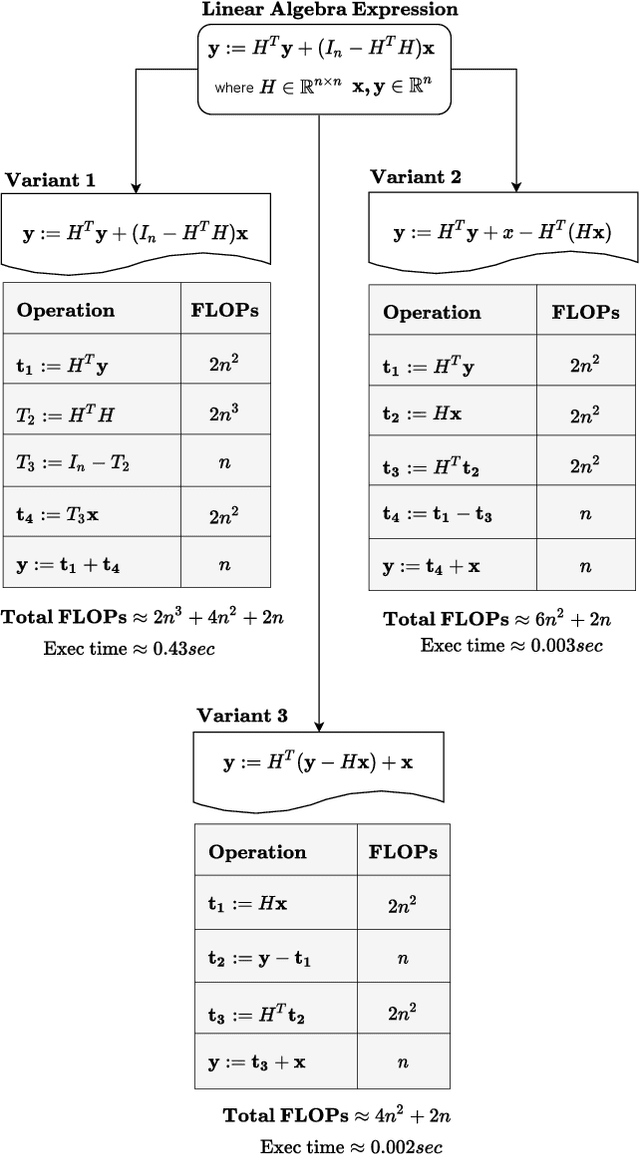
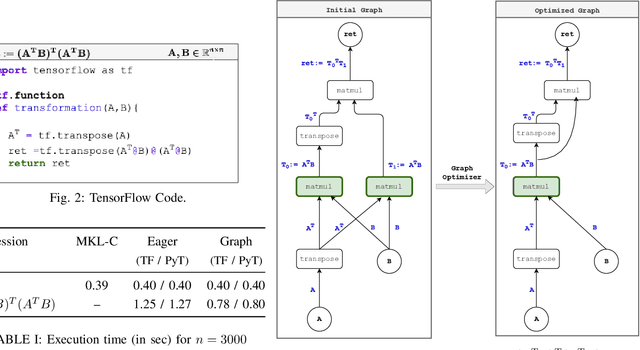
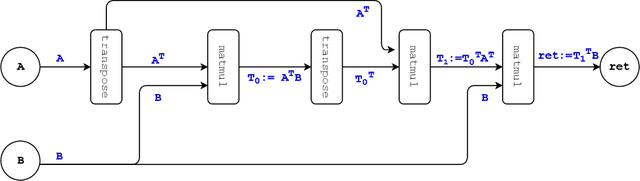
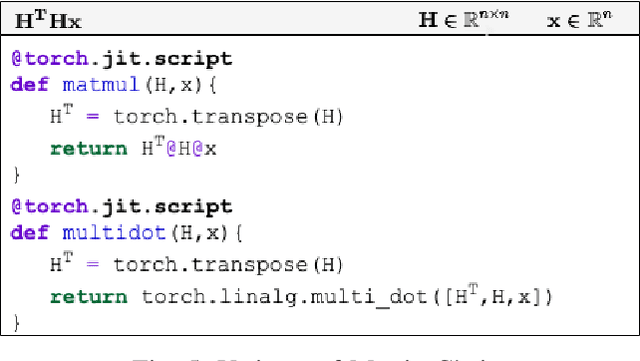
Linear algebra operations, which are ubiquitous in machine learning, form major performance bottlenecks. The High-Performance Computing community invests significant effort in the development of architecture-specific optimized kernels, such as those provided by the BLAS and LAPACK libraries, to speed up linear algebra operations. However, end users are progressively less likely to go through the error prone and time-consuming process of directly using said kernels; instead, frameworks such as TensorFlow (TF) and PyTorch (PyT), which facilitate the development of machine learning applications, are becoming more and more popular. Although such frameworks link to BLAS and LAPACK, it is not clear whether or not they make use of linear algebra knowledge to speed up computations. For this reason, in this paper we develop benchmarks to investigate the linear algebra optimization capabilities of TF and PyT. Our analyses reveal that a number of linear algebra optimizations are still missing; for instance, reducing the number of scalar operations by applying the distributive law, and automatically identifying the optimal parenthesization of a matrix chain. In this work, we focus on linear algebra computations in TF and PyT; we both expose opportunities for performance enhancement to the benefit of the developers of the frameworks and provide end users with guidelines on how to achieve performance gains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge