Networked Restless Multi-Armed Bandits for Mobile Interventions

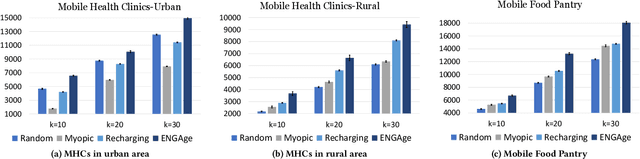
Motivated by a broad class of mobile intervention problems, we propose and study restless multi-armed bandits (RMABs) with network effects. In our model, arms are partially recharging and connected through a graph, so that pulling one arm also improves the state of neighboring arms, significantly extending the previously studied setting of fully recharging bandits with no network effects. In mobile interventions, network effects may arise due to regular population movements (such as commuting between home and work). We show that network effects in RMABs induce strong reward coupling that is not accounted for by existing solution methods. We propose a new solution approach for networked RMABs, exploiting concavity properties which arise under natural assumptions on the structure of intervention effects. We provide sufficient conditions for optimality of our approach in idealized settings and demonstrate that it empirically outperforms state-of-the art baselines in three mobile intervention domains using real-world graphs.

Efficient Algorithms for Finite Horizon and Streaming Restless Multi-Armed Bandit Problems

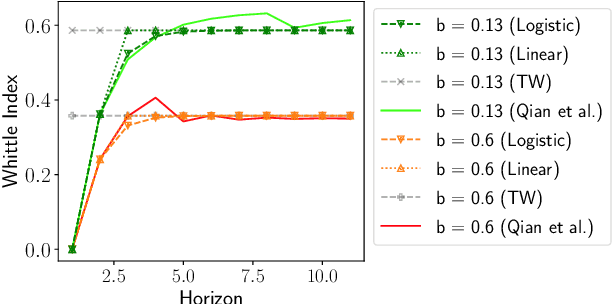
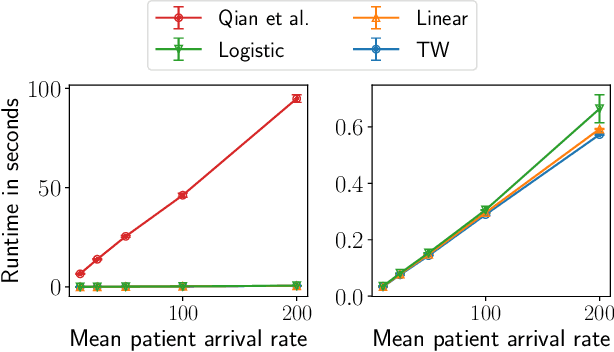
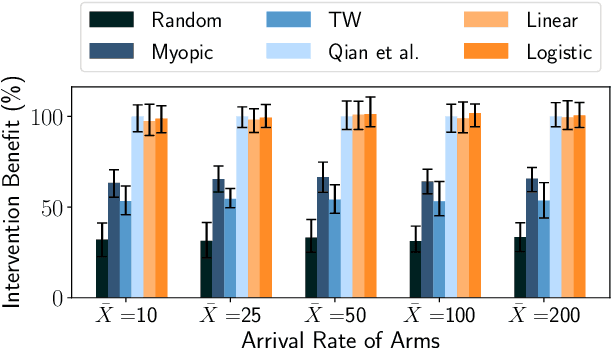
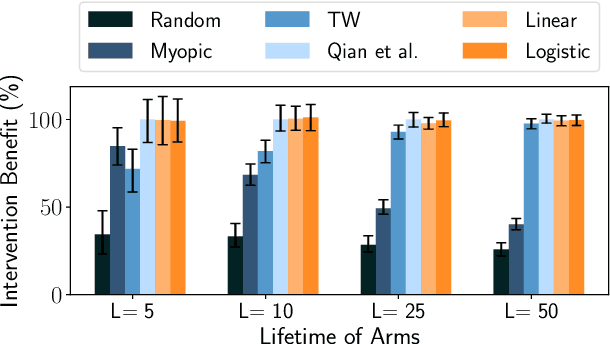
Restless Multi-Armed Bandits (RMABs) have been popularly used to model limited resource allocation problems. Recently, these have been employed for health monitoring and intervention planning problems. However, the existing approaches fail to account for the arrival of new patients and the departure of enrolled patients from a treatment program. To address this challenge, we formulate a streaming bandit (S-RMAB) framework, a generalization of RMABs where heterogeneous arms arrive and leave under possibly random streams. We propose a new and scalable approach to computing index-based solutions. We start by proving that index values decrease for short residual lifetimes, a phenomenon that we call index decay. We then provide algorithms designed to capture index decay without having to solve the costly finite horizon problem, thereby lowering the computational complexity compared to existing methods.We evaluate our approach via simulations run on real-world data obtained from a tuberculosis intervention planning task as well as multiple other synthetic domains. Our algorithms achieve an over 150x speed-up over existing methods in these tasks without loss in performance. These findings are robust across multiple domains.