Networked Restless Multi-Armed Bandits for Mobile Interventions
Paper and Code
Jan 28, 2022

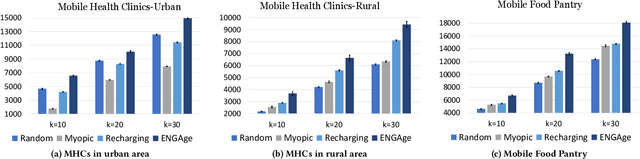

Motivated by a broad class of mobile intervention problems, we propose and study restless multi-armed bandits (RMABs) with network effects. In our model, arms are partially recharging and connected through a graph, so that pulling one arm also improves the state of neighboring arms, significantly extending the previously studied setting of fully recharging bandits with no network effects. In mobile interventions, network effects may arise due to regular population movements (such as commuting between home and work). We show that network effects in RMABs induce strong reward coupling that is not accounted for by existing solution methods. We propose a new solution approach for networked RMABs, exploiting concavity properties which arise under natural assumptions on the structure of intervention effects. We provide sufficient conditions for optimality of our approach in idealized settings and demonstrate that it empirically outperforms state-of-the art baselines in three mobile intervention domains using real-world graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge