Christine Zarges
Unlimited Budget Analysis of Randomised Search Heuristics
Sep 07, 2019
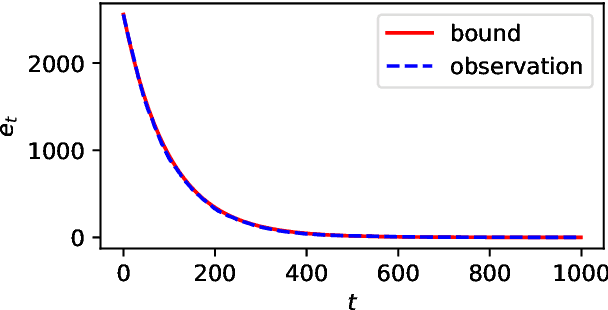
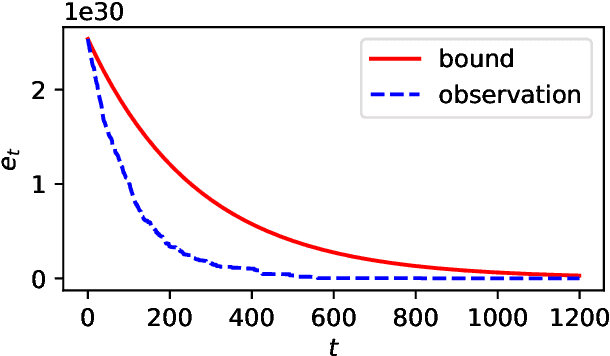

Abstract:Performance analysis of all kinds of randomised search heuristics is a rapidly growing and developing field. Run time and solution quality are two popular measures of the performance of these algorithms. The focus of this paper is on the solution quality an optimisation heuristic achieves, not on the time it takes to reach this goal, setting it far apart from runtime analysis. We contribute to its further development by introducing a novel analytical framework, called unlimited budget analysis, to derive the expected fitness value after arbitrary computational steps. It has its roots in the very recently introduced approximation error analysis and bears some similarity to fixed budget analysis. We present the framework, apply it to simple mutation-based algorithms, covering both, local and global search. We provide analytical results for a number of pseudo-Boolean functions for unlimited budget analysis and compare them to results derived within the fixed budget framework for the same algorithms and functions. There are also results of experiments to compare bounds obtained in the two different frameworks with the actual observed performance. The study show that unlimited budget analysis may lead to the same or more general estimation beyond fixed budget.
Optimizing Monotone Functions Can Be Difficult
Oct 14, 2010Abstract:Extending previous analyses on function classes like linear functions, we analyze how the simple (1+1) evolutionary algorithm optimizes pseudo-Boolean functions that are strictly monotone. Contrary to what one would expect, not all of these functions are easy to optimize. The choice of the constant $c$ in the mutation probability $p(n) = c/n$ can make a decisive difference. We show that if $c < 1$, then the (1+1) evolutionary algorithm finds the optimum of every such function in $\Theta(n \log n)$ iterations. For $c=1$, we can still prove an upper bound of $O(n^{3/2})$. However, for $c > 33$, we present a strictly monotone function such that the (1+1) evolutionary algorithm with overwhelming probability does not find the optimum within $2^{\Omega(n)}$ iterations. This is the first time that we observe that a constant factor change of the mutation probability changes the run-time by more than constant factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge